题目内容
已知:数列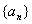 的前
的前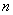 项和为
项和为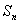 ,若
,若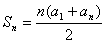 ,
,
(Ⅰ)求证: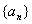 是等差数列;
是等差数列;
(Ⅱ)若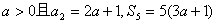 ,
,
求证: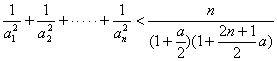
证明:(Ⅰ)当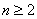 时,
时,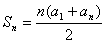 ①
①
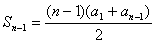 ②
②
①-②得: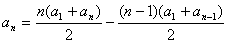
∴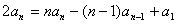 ③………………2分
③………………2分
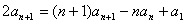 ④
④
④-③得:
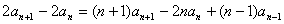 …………………………………………3分
…………………………………………3分
∴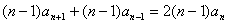 …………………………………………4分
…………………………………………4分
即: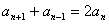
∴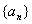 是等差数列;…………………………………………5分
是等差数列;…………………………………………5分
(Ⅱ)证法一:由 得:
得:

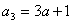 …………………………………………6分
…………………………………………6分
设公差为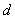 ,则
,则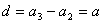 ,
,
∴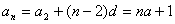 …………………………………………7分
…………………………………………7分
∴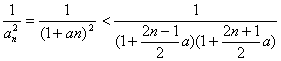
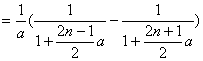 …………………………………………10分
…………………………………………10分
因此,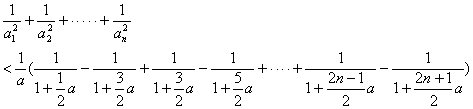
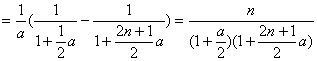 …………………………………12分
…………………………………12分
证法二:(数学归纳法)
当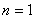 时,
时,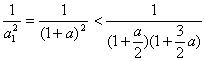 不等式成立,…………6分
不等式成立,…………6分
假设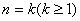 时,不等式成立,
时,不等式成立,
即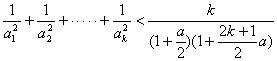 ………………………………7分
………………………………7分
那么 时,
时,
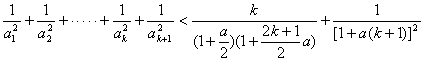 …………8分
…………8分
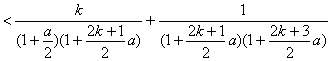
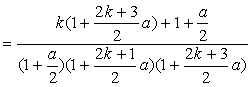
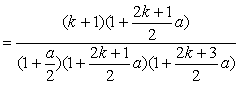
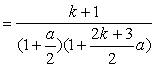 ………………………………………………………………11分
………………………………………………………………11分
即 时,不等式也成立,
时,不等式也成立,
由①②得,不等式恒成立. …………………………………………………………12分

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
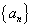 为等比数列,
为等比数列,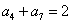 ,
,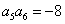 ,则
,则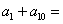 ( )
( ) D.-7
D.-7 中,若
中,若 ,
, ,
, .
.  ,
, ,
, ,
, ,则
,则
 B.
B. C.
C. D.
D.
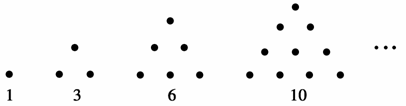
 ,可以推测:
,可以推测: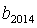 是数列
是数列 单调递增”是“
单调递增”是“ ”的什么条件
”的什么条件 是单位圆上的动点,且
是单位圆上的动点,且 ,单位圆的圆心为
,单位圆的圆心为 ,则
,则 ()
() B.
B. C.-1/2 D.
C.-1/2 D. 
 的图象大致是
的图象大致是
 ,B
,B ,C
,C ,则△ABC的形状是( )
,则△ABC的形状是( )