题目内容
本题满分12分)
在直角坐标平面内,已知点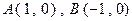 ,动点
,动点 满足
满足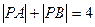 .
.
(1)求动点 的轨迹
的轨迹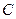 的方程;
的方程;
(2)过点 作直线
作直线 与轨迹
与轨迹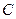 交于
交于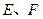 两点,线段
两点,线段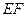 的中点为
的中点为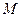 ,轨迹
,轨迹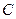 的右端点为点N,求直线MN的斜率
的右端点为点N,求直线MN的斜率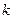 的取值范围.
的取值范围.
解: (1)由椭圆的定义知,点P的轨迹是以点A、B为焦点的椭圆,……….……….1分
且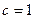 ,
,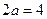 ∴
∴ ……….……….3分
……….……….3分
∴动点 的轨迹
的轨迹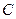 的方程是
的方程是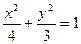 . ………………… 4分
. ………………… 4分
(2)解法一:依题意,直线
 过点
过点 且斜率不为零,故可设其方程为
且斜率不为零,故可设其方程为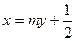 ,
,
由方程组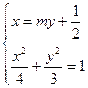 消去
消去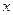 ,并整理得
,并整理得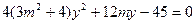 ……….……….5分
……….……….5分
(2)当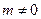 时,
时, 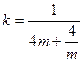
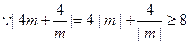
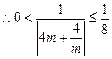 .
.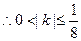 .
.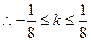 且
且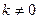 . …………………………… 11分
. …………………………… 11分
综合(1)、(2)可知直线MN的斜率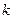 的取值范围是:
的取值范围是: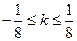 .……………… 12分
.……………… 12分
解法二:依题意,直线 过点
过点 且斜率不为零.
且斜率不为零.
(1)当直线 与
与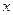 轴垂直
轴垂直 时,
时,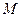 点的坐标为
点的坐标为 ,此时,
,此时,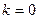 ; …………5分
; …………5分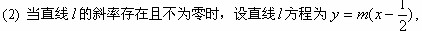

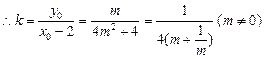 , …………… 9分
, …………… 9分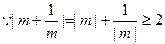
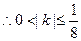 .
.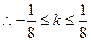 且
且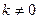 . ………………………………………… 11分
. ………………………………………… 11分
综合(1)、(2)可知直线MN的斜率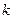 的取值范围是:
的取值范围是: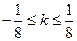 .………… 12分
.………… 12分
解析

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 中,
中,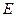 、
、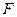 、
、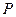 分别是
分别是 、
、 、
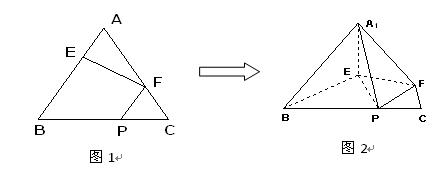
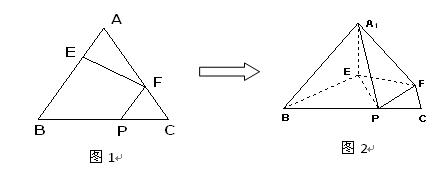
、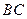 边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△
边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△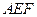 沿
沿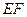 折起到
折起到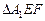 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2) ,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合)。过D1和CC1的平面与AB交于D。
,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合)。过D1和CC1的平面与AB交于D。
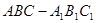 中,
中, ,直线
,直线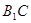 与平面
与平面 成
成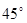 角;
角;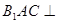 平面
平面 ;
; 的正弦值.
的正弦值.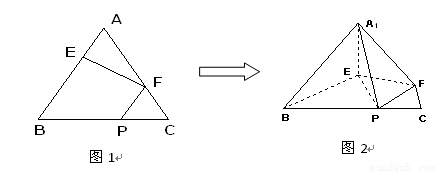
 中,
中, 、
、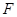 、
、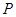 分别是
分别是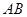 、
、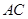 、
、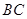 边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△
边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△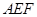 沿
沿 折起到
折起到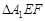 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)