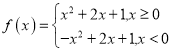题目内容
【题目】设函数![]() (
(![]() ,且
,且![]() )是定义域为R的奇函数.
)是定义域为R的奇函数.
(1)求t的值;
(2)若![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 恒成立的实数k的取值范围;
恒成立的实数k的取值范围;
(3)若函数![]() 的图象过点
的图象过点![]() ,是否存在正数m(
,是否存在正数m(![]() ),使函数
),使函数![]() 在
在![]() 上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
【答案】(1)![]() ,(2)
,(2)![]() ,(3)不存在,理由见解析
,(3)不存在,理由见解析
【解析】
(1)结合函数奇偶性,利用![]() 可求;
可求;
(2)根据![]() 可得
可得![]() ,结合奇偶性和单调性把所求解的不等式转化为二次不等式,然后进行求解;
,结合奇偶性和单调性把所求解的不等式转化为二次不等式,然后进行求解;
(3)根据函数图象过点![]() 可得
可得![]() ,利用换元法进行求解.
,利用换元法进行求解.
(1)![]() 是定义域为R的奇函数,
是定义域为R的奇函数,
![]() ,
,
![]() ;经检验知符合题意.
;经检验知符合题意.
(2)由(1)得![]() ,
,
![]() 得
得![]() ,又
,又![]()
![]() ,
,
由![]() 得
得![]() ,
,
![]() 为奇函数,
为奇函数,
![]() ,
,
![]() ,
,![]() 为R上的增函数,
为R上的增函数,
![]() 对一切
对一切![]() 恒成立,即
恒成立,即![]() 对一切
对一切![]() 恒成立,
恒成立,
故![]() 解得
解得![]() .
.
(3)函数![]() 的图象过点
的图象过点![]() ,
,
![]() ,假设存在正数m,且
,假设存在正数m,且![]() 符合题意,
符合题意,
由![]() 得
得
![]() ,
,
设![]() 则
则![]() ,
,
![]() ,
,
![]() ,记
,记![]() ,
,
∵函数![]() 在
在![]() 上的最大值为0,
上的最大值为0,
∴(i)若![]() 时,则函数
时,则函数![]() 在
在![]() 有最小值为1,
有最小值为1,
由于对称轴![]() ,
,
![]() ,不合题意.
,不合题意.
(ii)若![]() 时,则函数
时,则函数![]() 在
在![]() 上恒成立,且最大值为1,最小值大于0,
上恒成立,且最大值为1,最小值大于0,
①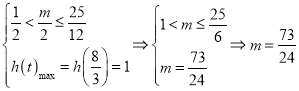 ,
,
而此时![]() ,又
,又![]() ,
,
故![]() 在
在![]() 无意义,
无意义,
所以![]() 应舍去;
应舍去;
②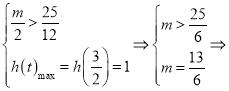 m无解,
m无解,
综上所述:故不存在正数m,使函数![]() 在
在![]() 上的最大值为0.
上的最大值为0.

练习册系列答案
相关题目