Question

【题目】已知椭圆： 的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线： 与椭圆有且只有一个公共点．

（Ⅰ）求椭圆的方程及点的坐标；

（Ⅱ）设是坐标原点，直线平行于，与椭圆交于不同的两点、，且与直线交于点，证明：存在常数，使得，并求的值．

Answer 1

【答案】（Ⅰ），点T坐标为（2,1）；（Ⅱ）.

【解析】试题分析：本题考查椭圆的标准方程及其几何性质，考查学生的分析问题、解决问题的能力和数形结合的思想.第（Ⅰ）问，利用直线和椭圆只有一个公共点，联立方程，消去y得关于x的方程有两个相等的实数根，解出b的值，从而得到椭圆E的方程；第（Ⅱ）问，利用椭圆的几何性质，数形结合，根据根与系数的关系，进行求解.

试题解析：（Ⅰ）由已知， ，则椭圆E的方程为.

由方程组得.①

方程①的判别式为，由，得，

此时方程①的解为，

所以椭圆E的方程为.

点T坐标为（2,1）.

（Ⅱ）由已知可设直线的方程为，

由方程组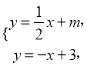可得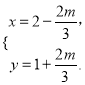

所以P点坐标为（），.

设点A，B的坐标分别为.

由方程组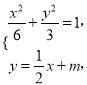可得.②

方程②的判别式为，由，解得.

由②得.

所以，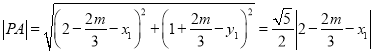

同理，

所以

.

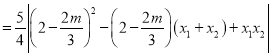
故存在常数，使得.