题目内容
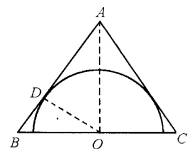
一个等腰三角形底边上的高等于4，底边两端的坐标是(-3，0)、(3，0)，求它的外接圆方程.
【探究】 由题设可知圆心在腰和底边的中垂线上，可由任意两条中垂线求得交点，即圆心，继而由圆心及一端点坐标求得半径长.本题也可以根据图形，利用圆和三角形的几何性质求解，利用数形结合的数学思想解决问题，计算相对简单.
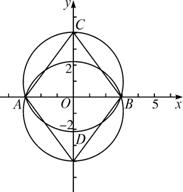
解法一：底边端点关于原点对称，所以底边的中垂线方程为x=0，
底边上的高等于4，说明第三个点的坐标为(0，4)， ①
一腰中垂线的方程为y-2=
(x
)或y+2=
， ②
方程①②联立得圆心坐标为(0，
)或(0，
)，半径为
.故所求圆的方程为x2+(y+
)2=
或x2+(y-
)2=
.
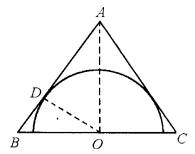
解法二：由题意，结合图形可知：
利用射影定理有AO2=CO·DO，即32=4(2R-4)(R为三角形外接圆半径)，解得R=
，圆心坐标为(0，
)或(0，
)，即(0，
)或(0，
).
所以圆的方程为x2+(y+
)2=
或x2+(y-
)2=
.
【规律总结】 求圆的方程，就是要确定圆心和半径，圆的标准方程中有三个未知量a、b、r，故确定一个圆需要三个独立的条件，一般利用待定系数法确定.这需要把题目中的已知条件一一转化为关于圆心坐标和半径的方程，利用方程组获得圆心和半径的值，进而确定圆的方程.其基本步骤为:(1)根据题意，设所求的圆的标准方程为(x-a)2+(y-b)2=r2；(2)根据已知条件，建立关于a、b、r的方程组；(3)解方程组，求出a、b、r的值，并把它们代入所设的方程中去，就得到所求圆的方程.不过有时利用圆的几何性质解题，会有更简捷的解题途径.
练习册系列答案
名校课堂系列答案
相关题目
