题目内容
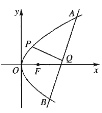
【题目】已知椭圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,一动圆在
,一动圆在![]() 轴右侧与
轴右侧与![]() 轴相切,同时与圆
轴相切,同时与圆![]() 相外切,此动圆的圆心轨迹为曲线
相外切,此动圆的圆心轨迹为曲线![]() ,椭圆
,椭圆![]() 与曲线
与曲线![]() 有相同的焦点.
有相同的焦点.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 与椭圆
与椭圆![]() 相交于第一象限点
相交于第一象限点![]() ,且
,且![]() ,求椭圆
,求椭圆![]() 的标准方程;
的标准方程;
(3)在(2)的条件下,如果椭圆![]() 的左顶点为
的左顶点为![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与直线
与直线![]() :
:![]() 分别交于
分别交于![]() ,
,![]() 两点,证明:四边形
两点,证明:四边形![]() 的对角线的交点是椭圆
的对角线的交点是椭圆![]() 的右顶点.
的右顶点.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)设动圆圆心的坐标为![]() ,
,![]() ,计算化简得到答案.
,计算化简得到答案.
(2)计算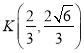 ,则
,则![]() ,得到答案.
,得到答案.
(3)计算![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为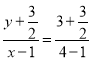 ,令
,令![]() ,得
,得![]() ,得到答案.
,得到答案.
(1)设动圆圆心的坐标为![]() ,因为动圆在
,因为动圆在![]() 轴右侧与
轴右侧与![]() 轴相切,同时与圆
轴相切,同时与圆![]() 相外切,所以
相外切,所以![]() ,所以
,所以![]() ,化简整理得
,化简整理得![]() ,
,
曲线![]() 的方程为
的方程为![]() .
.
(2)依题意,![]() ,
,![]() ,可得
,可得![]() ,故
,故![]() 点坐标为
点坐标为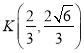 ,
,
椭圆的另一焦点为![]() ,
,
由两点间的距离可得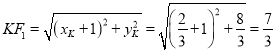 ,
,
又由椭圆的定义得![]() ,
,![]() .
.
所以![]() ,所以椭圆
,所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(3)由(2)知![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
根据椭圆的对称性,当直线![]() 轴时,四边形
轴时,四边形![]() 是等腰梯形,对角线的交点在
是等腰梯形,对角线的交点在![]() 轴上,此时直线
轴上,此时直线![]() 的方程为
的方程为![]() ,
,
由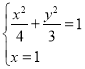 ,
,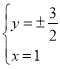 ,不妨取
,不妨取![]() ,
,![]() ,
,
故直线![]() 的方程为
的方程为![]() ,将
,将![]() 代入得
代入得![]() ,
,
所以直线![]() 的方程为
的方程为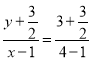 ,令
,令![]() ,得
,得![]() ,
,
即直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,此时恰好为椭圆的右顶点.
,此时恰好为椭圆的右顶点.

练习册系列答案
相关题目