题目内容
抛物线![]() 的准线的方程为
的准线的方程为![]() ,该抛物线上的每个点到准线
,该抛物线上的每个点到准线![]() 的距离都与到定点
的距离都与到定点![]() 的距离相等,圆
的距离相等,圆![]() 是以
是以![]() 为圆心,同时与直线
为圆心,同时与直线![]() 和
和![]() 相切的圆,
相切的圆,
(Ⅰ)求定点![]() 的坐标;
的坐标;
(Ⅱ)是否存在一条直线![]() 同时满足下列条件:
同时满足下列条件:
① ![]() 分别与直线
分别与直线![]() 和
和![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() 中点为
中点为![]() ;
;
② ![]() 被圆
被圆![]() 截得的弦长为2.
截得的弦长为2.
![]()
![]() ,不存在
,不存在
解析:
(1)![]() 抛物线
抛物线![]() 的准线的方程为
的准线的方程为![]()
![]()
根据抛物线的定义可知点N是抛物线的焦点,
![]() 定点N的坐标为
定点N的坐标为![]()
(2)假设存在直线![]() 满足两个条件,显然
满足两个条件,显然![]() 斜率存在,
斜率存在,
![]() 设
设![]() 的方程为
的方程为![]() ,
,![]() 以N为圆心,同时与直线
以N为圆心,同时与直线![]() 相切的圆N的半径为
相切的圆N的半径为![]() ,
,
方法1:![]()
![]() 被圆N截得的弦长为2,
被圆N截得的弦长为2,![]() 圆心到直线的距离等于1,
圆心到直线的距离等于1,
即![]() ,解得
,解得![]() ,
,
当![]() 时,显然不合AB中点为
时,显然不合AB中点为![]() 的条件,矛盾!当
的条件,矛盾!当![]() 时,
时,![]() 的方程为
的方程为![]()
由![]() ,解得点A坐标为
,解得点A坐标为![]() ,
,
由![]() ,解得点B坐标为
,解得点B坐标为![]() ,
,
显然AB中点不是![]() ,矛盾!
,矛盾! ![]() 不存在满足条件的直线
不存在满足条件的直线![]() .
.
方法2:由![]() ,解得点A坐标为
,解得点A坐标为![]() ,由
,由![]() ,解得点B坐标为
,解得点B坐标为![]() ,
,
![]() AB中点为
AB中点为![]() ,
,![]()
![]() ,解得
,解得![]() ,
,
![]()
![]() 的方程为
的方程为![]() ,
,
圆心N到直线![]() 的距离
的距离![]() ,
,
![]()
![]() 被圆N截得的弦长为2,
被圆N截得的弦长为2,![]() 圆心到直线的距离等于1,矛盾!
圆心到直线的距离等于1,矛盾!
![]() 不存在满足条件的直线
不存在满足条件的直线![]() .
.
方法3:假设A点的坐标为![]() ,
,
![]() AB中点为
AB中点为![]() ,
,![]() B点的坐标为
B点的坐标为![]() ,
,
又点B 在直线![]() 上,
上,![]()
![]() ,
,
![]()
![]() A点的坐标为
A点的坐标为![]() ,直线
,直线![]() 的斜率为4,
的斜率为4,
![]()
![]() 的方程为
的方程为![]() ,
,
圆心N到直线![]() 的距离
的距离![]() ,
,
![]()
![]() 被圆N截得的弦长为2,
被圆N截得的弦长为2,![]() 圆心到直线的距离等于1,矛盾!
圆心到直线的距离等于1,矛盾!
![]() 不存在满足条件的直线
不存在满足条件的直线![]() .
.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 的准线的方程为
的准线的方程为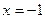 ,过点
,过点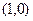 作倾斜角为
作倾斜角为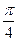 的直线
的直线 交该抛物线于两点
交该抛物线于两点 ,
, .求:(1)
.求:(1)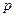 的值;(2)弦长
的值;(2)弦长
 的准线的方程为
的准线的方程为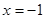 ,过点
,过点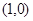 作倾斜角为
作倾斜角为 的直线
的直线 交该抛物线于两点
交该抛物线于两点 ,
, .求:(1)
.求:(1)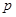 的值;(2)弦长
的值;(2)弦长