题目内容
对于空间四点A、B、C、D,命题p: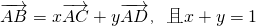 ;命题q:A、B、C、D四点共面,则命题p是命题q的
;命题q:A、B、C、D四点共面,则命题p是命题q的
- A.充分不必要条件
- B.必要不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
A
分析:根据命题p可得 共面,从而可得命题q:A、B、C、D四点共面成立; 若 命题q:A、B、C、D四点共面,则A、B、C、D四点有可能在同一条直线上,虽有
共面,从而可得命题q:A、B、C、D四点共面成立; 若 命题q:A、B、C、D四点共面,则A、B、C、D四点有可能在同一条直线上,虽有 ,但x+y不一定等于1,故不能推出命题p成立,由此可得结论.
,但x+y不一定等于1,故不能推出命题p成立,由此可得结论.
解答:根据命题p: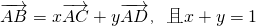 ,可得
,可得 共面,从而可得命题q:A、B、C、D四点共面成立,
共面,从而可得命题q:A、B、C、D四点共面成立,
故命题p是命题q的充分条件.
根据命题q:A、B、C、D四点共面,可得A、B、C、D四点有可能在同一条直线上,若 ,
,
则x+y不一定等于1,
故命题p不是命题q的必要条件.
综上,可得命题p是命题q的充分不必要条件.
故选:A.
点评:本题主要考察充分条件、必要条件、充要条件的定义,平面向量基本定理及其几何意义,属于基础题.
分析:根据命题p可得
 共面,从而可得命题q:A、B、C、D四点共面成立; 若 命题q:A、B、C、D四点共面,则A、B、C、D四点有可能在同一条直线上,虽有
共面,从而可得命题q:A、B、C、D四点共面成立; 若 命题q:A、B、C、D四点共面,则A、B、C、D四点有可能在同一条直线上,虽有 ,但x+y不一定等于1,故不能推出命题p成立,由此可得结论.
,但x+y不一定等于1,故不能推出命题p成立,由此可得结论.解答:根据命题p:
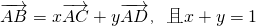 ,可得
,可得 共面,从而可得命题q:A、B、C、D四点共面成立,
共面,从而可得命题q:A、B、C、D四点共面成立,故命题p是命题q的充分条件.
根据命题q:A、B、C、D四点共面,可得A、B、C、D四点有可能在同一条直线上,若
 ,
,则x+y不一定等于1,
故命题p不是命题q的必要条件.
综上,可得命题p是命题q的充分不必要条件.
故选:A.
点评:本题主要考察充分条件、必要条件、充要条件的定义,平面向量基本定理及其几何意义,属于基础题.

练习册系列答案
相关题目
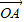 =x
=x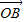 +y
+y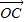 +z
+z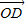 .
.