题目内容
如图正四面体D-ABC中，P∈面DBA，则在平面DAB内过点P与直线BC成60°角的直线共有
- A.0条
- B.1条
- C.2条
- D.3条
C
分析：由于正四面体D-ABC各个面都是正三角形，则在平面DAB内过B点有两条直线DB、AB与BC成60°．
解答：在平面DAB内过点B与直线BC成60°角的直线共有2条，
因此在平面DAB内过点P与直线BC成60°角的直线共有2条，
故选C．
点评：此题主要考查学生立体几何中异面直线之间角度问题．
分析：由于正四面体D-ABC各个面都是正三角形，则在平面DAB内过B点有两条直线DB、AB与BC成60°．
解答：在平面DAB内过点B与直线BC成60°角的直线共有2条，
因此在平面DAB内过点P与直线BC成60°角的直线共有2条，
故选C．
点评：此题主要考查学生立体几何中异面直线之间角度问题．
练习册系列答案
相关题目
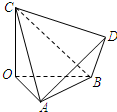如图，四面体OABC的三条棱OA，OB，OC两两垂直，OA=OB=2，OC=3，D为四面体OABC外一点．给出下列命题．
