题目内容
已知各项均不相等的等差数列 的前四项和为14,且
的前四项和为14,且 恰为等比数列
恰为等比数列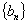 的前三项.
的前三项.
(1)分别求数列 ,
,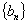 的前
的前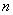 项和
项和 ,
, ;
;
(2)记为数列 的前
的前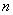 项和为
项和为 ,设
,设 ,求证:
,求证: .
.
解析:(1)设公差为d,则 ,
,
解得d=1或d=0(舍去),a1=2,
所以an=n+1,Sn= ,bn=2n,Tn=2n+1-2.(4分)
,bn=2n,Tn=2n+1-2.(4分)
(2)因为Kn=2·21+3·22+…+(n+1)·2n,①
故2Kn=2·22+3·23+…+n·2n+(n+1)·2n+1,②
①-②,得
-Kn=2·21+22+23+…+2n-(n+1)·2n+1,
所以Kn=n·2n+1,则cn= =
= ,
,
cn+1-cn= -
- =
= >0,
>0,
所以cn+1>cn(n∈N*).

练习册系列答案
相关题目
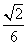 .
.
 的对称轴方程为x=______________.
的对称轴方程为x=______________. ,则
,则 等于 ( ).
等于 ( ). B.
B. C.
C. D.
D.
 ,
, .
. ,求
,求 的值;
的值; 与
与 的夹角为钝角,求
的夹角为钝角,求 的不等式
的不等式 的解集
的解集 ,则
,则 的值为_________.
的值为_________. ) B.(
) B.( ,
, )
) 的通项公式为
的通项公式为 ,则由此数列的偶数项所组成的新数列的
,则由此数列的偶数项所组成的新数列的 项和
项和
 B.
B. C.
C. D.
D.