题目内容
在锐角△ABC中,角A、B、C所对的边分别为a、b、c.且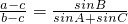 .
.
(1)求角A的大小及角B的取值范围;
(2)若 ,求b2+c2的取值范围.
,求b2+c2的取值范围.
解:(1)由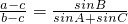 得
得 即b2+c2-a2=bc
即b2+c2-a2=bc
得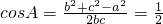 ,A∈(0,
,A∈(0, )
)
故 .
.
又∵△ABC是锐角三角形,∴ ,即
,即 ,得
,得
故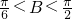 .
.
(2)由 ,得
,得 ,∴b=2sinB,c=2sinC
,∴b=2sinB,c=2sinC
∵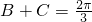 ,∴
,∴
∴b2+c2=4(sin2B+sin2C)=2(1-cos2B+1-cos2C)=4-2(cos2B+cos2C)= =
= =
=
∵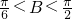 ,∴
,∴
∴当 时,即
时,即 时,b2+c2取得最大值6.
时,b2+c2取得最大值6.
当 时,即
时,即 时,b2+c2取得最小值5.
时,b2+c2取得最小值5.
故所求b2+c2的取值范围是(5,6].
分析:(1)利用正弦定理,将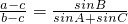 中的角化为边,得b2+c2-a2=bc,再利用余弦定理即可得角A,再由三角形ABC为锐角三角形,求得角B的取值范围;
中的角化为边,得b2+c2-a2=bc,再利用余弦定理即可得角A,再由三角形ABC为锐角三角形,求得角B的取值范围;
(2)利用正弦定理将b2+c2转化为三角函数,再利用三角变换公式将函数化为y=Asin(ωx+φ)型函数,再利用(1)中角B的取值范围求函数值域即可
点评:本题主要考查了正弦定理和余弦定理的应用,三角函数的值域的求法,利用定理实现边角间的互化是解决本题的关键,
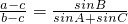 得
得 即b2+c2-a2=bc
即b2+c2-a2=bc得
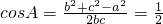 ,A∈(0,
,A∈(0, )
)故
 .
.又∵△ABC是锐角三角形,∴
 ,即
,即 ,得
,得
故
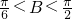 .
.(2)由
 ,得
,得 ,∴b=2sinB,c=2sinC
,∴b=2sinB,c=2sinC∵
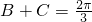 ,∴
,∴
∴b2+c2=4(sin2B+sin2C)=2(1-cos2B+1-cos2C)=4-2(cos2B+cos2C)=
 =
= =
=
∵
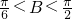 ,∴
,∴
∴当
 时,即
时,即 时,b2+c2取得最大值6.
时,b2+c2取得最大值6.当
 时,即
时,即 时,b2+c2取得最小值5.
时,b2+c2取得最小值5.故所求b2+c2的取值范围是(5,6].
分析:(1)利用正弦定理,将
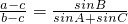 中的角化为边,得b2+c2-a2=bc,再利用余弦定理即可得角A,再由三角形ABC为锐角三角形,求得角B的取值范围;
中的角化为边,得b2+c2-a2=bc,再利用余弦定理即可得角A,再由三角形ABC为锐角三角形,求得角B的取值范围;(2)利用正弦定理将b2+c2转化为三角函数,再利用三角变换公式将函数化为y=Asin(ωx+φ)型函数,再利用(1)中角B的取值范围求函数值域即可
点评:本题主要考查了正弦定理和余弦定理的应用,三角函数的值域的求法,利用定理实现边角间的互化是解决本题的关键,

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目