题目内容
△ABC中,A(0,1),AB边上的高CD所在直线的方程为x+2y-4=0,AC边上的中线BE所在直线的方程为2x+y-3=0.
(1)求直线AB的方程;
(2)求直线BC的方程;
(3)求△BDE的面积.
(1)求直线AB的方程;
(2)求直线BC的方程;
(3)求△BDE的面积.
分析:(1)由CD所在直线的方程求出直线AB的斜率,再由点斜式写出AB的直线方程;
(2)先求出点B,点C的坐标,再写出BC的直线方程;
(3)由点到直线的距离求出E到AB的距离d,以及B到CD的距离BD,计算S△BDE即可.
或求出BE,D到BE的距离d,计算S△BDE.
(2)先求出点B,点C的坐标,再写出BC的直线方程;
(3)由点到直线的距离求出E到AB的距离d,以及B到CD的距离BD,计算S△BDE即可.
或求出BE,D到BE的距离d,计算S△BDE.
解答:解:(1)∵CD所在直线的方程为x+2y-4=0,
∴直线AB的斜率为2,
∴AB边所在的直线方程为y-1=2(x-0),即2x-y+1=0;
(2)由
,得
,
即直线AB与AC边中线BE的交点为B(
,2);
设C(m,n),
则由已知条件得
,
解得
,∴C(2,1);
∴所以BC边所在的直线方程为
=
,即2x+3y-7=0;
(3)∵E是AC的中点,∴E(1,1),
∴E到AB的距离为:d=
;
又点B到CD的距离为:BD=
,
∴S△BDE=
•d•BD=
.
另解:∵E是AC的中点,∴E(1,1),
∴BE=
,
由
,
得
,∴D(
,
),
∴D到BE的距离为:d=
,
∴S△BDE=
•d•BE=
.
∴直线AB的斜率为2,
∴AB边所在的直线方程为y-1=2(x-0),即2x-y+1=0;
(2)由
|
|
即直线AB与AC边中线BE的交点为B(
| 1 |
| 2 |
设C(m,n),
则由已知条件得
|
解得
|
∴所以BC边所在的直线方程为
x-
| ||
2-
|
| y-2 |
| 1-2 |
(3)∵E是AC的中点,∴E(1,1),
∴E到AB的距离为:d=
| 2 | ||
|
又点B到CD的距离为:BD=
| 1 | ||
2
|
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 10 |
另解:∵E是AC的中点,∴E(1,1),
∴BE=
| ||
| 2 |
由
|
得
|
| 2 |
| 5 |
| 9 |
| 5 |
∴D到BE的距离为:d=
| 2 | ||
5
|
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 10 |
点评:本题考查了求直线的方程以及点到直线的距离公式的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图△ABC中,A(0,1),B(-2,2),C(2,6),写出△ABC区域所表示的二元一次不等组.
如图△ABC中,A(0,1),B(-2,2),C(2,6),写出△ABC区域所表示的二元一次不等组.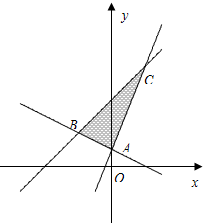 如图△ABC中,A(0,1),B(-2,2),C(2,6).
如图△ABC中,A(0,1),B(-2,2),C(2,6).