题目内容
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) |  | 30 | 25 |  | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.(注:将频率视为概率)
(Ⅰ)
 的分布为
的分布为 X 1 1.5 2 2.5 3 P 




X的数学期望为 (Ⅱ)
(Ⅱ)
解析试题分析:解:(1)由已知,得 所以
所以
该超市所有顾客一次购物的结算时间组成一个总体,所以收集的100位顾客一次购物的结算时间可视为总体的一个容量随机样本,将频率视为概率得




 的分布为
的分布为 X 1 1.5 2 2.5 3 P 




X的数学期望为
(Ⅱ)记A为事件“该顾客结算前的等候时间不超过2.5分钟”, 为该顾客前面第
为该顾客前面第 位顾客的结算时间,则
位顾客的结算时间,则
由于顾客的结算相互独立,且 的分布列都与X的分布列相同,所以
的分布列都与X的分布列相同,所以

故该顾客结算前的等候时间不超过2.5分钟的概率为 .
.
考点:分布列与数学期望;概率
点评:分布列是求出数学期望的前提,因而需写好分布列,而分布列关键是求出概率,当写完分布列,可以结合概率总和为1的特点检验分布列是否正确。

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
(12分)某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(Ⅰ)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(Ⅱ)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2100 | 1027 | 376 | 697 |
| 运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2100 | 1051 | 696 | 353 |

某单位实行休年假制度三年来, 名职工休年假的次数进行的调查统计结果如下表所示:
名职工休年假的次数进行的调查统计结果如下表所示:
| 休假次数 |  |  |  |  |
| 人数 | 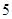 |  |  |  |
⑴从该单位任选两名职工,用
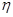 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数 ,在区间
,在区间 ,
, 上有且只有一个零点”为事件
上有且只有一个零点”为事件 ,求事件
,求事件 发生的概率
发生的概率 ;
;⑵从该单位任选两名职工,用
 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
. 某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间(单位:分钟)进行了统计,如下表.若视频率为概率,请用有关知识解决下列问题.
| 病症及代号 | 普通病症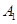 | 复诊病症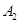 | 常见病症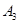 | 疑难病症 | 特殊病症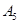 |
| 人数 | 100 | 300 | 200 | 300 | 100 |
| 每人就诊时间(单位:分钟) | 3 | 4 | 5 | 6 | 7 |
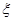 表示某病人诊断所需时间,求
表示某病人诊断所需时间,求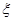 的数学期望.
的数学期望.并以此估计专家一上午(按3小时计算)可诊断多少病人;
某病人按序号排在第三号就诊,设他等待的时间为
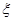 ,求
,求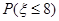 ;
;求专家诊断完三个病人恰好用了一刻钟的概率.
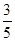 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是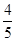 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用 表示张同学答对题的个数,求
表示张同学答对题的个数,求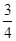 、
、 、
、 .指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
.指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.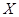 ,求
,求