题目内容
已知在等比数列{an}中，各项均为正数，且a1=1，a1+a2+a3=7则数列{an}的通项公式是an=________；前n项和Sn=________．
2n-1 2n-1
分析：利用等比数列的通项公式和前n项和公式即可求出．
解答：设等比数列{an}的公比为q，∵各项均为正数，∴q＞0．
∵a1=1，a1+a2+a3=7，
∴1+q+q2=7，化为q2+q-6=0，又q＞0，∴q=2．
∴
．
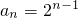Sn=1+2+22+…+2n-1=
=2n-1．
故答案为2n-1，2n-1．
点评：熟练掌握等比数列的通项公式和前n项和公式是解题的关键．
分析：利用等比数列的通项公式和前n项和公式即可求出．
解答：设等比数列{an}的公比为q，∵各项均为正数，∴q＞0．
∵a1=1，a1+a2+a3=7，
∴1+q+q2=7，化为q2+q-6=0，又q＞0，∴q=2．
∴
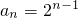．Sn=1+2+22+…+2n-1=
=2n-1．故答案为2n-1，2n-1．
点评：熟练掌握等比数列的通项公式和前n项和公式是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知在等比数列{an}中，a1+a3=10，a4+a6=
，则等比数列{an}的公比q的值为（ ）
| 5 |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
| D、8 |
已知在等比数列{an}中，Sn为其前n项和，且a4=2S3+3，a5=2S4+3，则此数列的公比q为（ ）
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|