题目内容
设函数y=xsinx+cosx的图像上的点(x0,y0)的切线的斜率为k,若k=g(x0),则函数k=g(x0)的图像大致为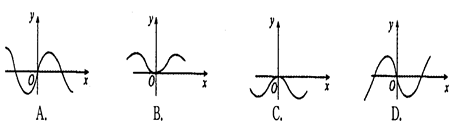
A
解析试题分析:∵ ,∴
,∴ ,∴
,∴ ,∵g(-x)=-xcos(-x)=-xcosx=-g(x),∴函数y=g(x)是奇函数,图象关于原点对称,再根据当0<x<
,∵g(-x)=-xcos(-x)=-xcosx=-g(x),∴函数y=g(x)是奇函数,图象关于原点对称,再根据当0<x< 时,x与cosx均为正值,可得:0<x<
时,x与cosx均为正值,可得:0<x< 时,f(x)>0,因此符合题意的图象只有A,选A
时,f(x)>0,因此符合题意的图象只有A,选A
考点:本题考查了导数的运用及函数图象的运用
点评:本题以含有三角函数表达式的函数为载体,考查了导数的几何意义、函数奇偶性与图象间的联系等知识点,属于基础题

练习册系列答案
相关题目
函数 的图象与直线
的图象与直线 的公共点数目是( )
的公共点数目是( )
A. | B. | C. 或 或 | D. 或 或 |
已知函数 是R上的单调增函数且为奇函数,数列
是R上的单调增函数且为奇函数,数列 是等差数列,
是等差数列, >0,则
>0,则 的值 ( )
的值 ( )
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
已知函数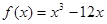 ,若
,若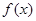 在区间
在区间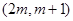 上单调递减,则实数
上单调递减,则实数 的取值范围是( )
的取值范围是( )
A.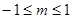 | B.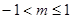 | C.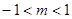 | D.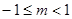 |
定义在R上的奇函数f(x),当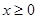 时,
时, ,则函数
,则函数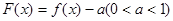 的所有零点之和为( )
的所有零点之和为( )
A.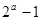 | B.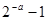 | C. | D.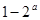 |
已知函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为
A. | B. | C. | D. |
已知 是偶函数,且
是偶函数,且 ,那么
,那么 的值为( )。
的值为( )。
| A.5 | B.10 | C. 8 | D.不确定 |
已知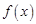 是
是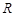 上的奇函数,且满足
上的奇函数,且满足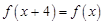 ,当
,当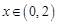 时,
时,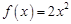 ,则
,则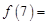 ( )
( )
| A.-2 | B.2 | C.4 | D.-4 |