题目内容
已知函数 是R上的单调增函数且为奇函数,数列
是R上的单调增函数且为奇函数,数列 是等差数列,
是等差数列, >0,则
>0,则 的值 ( )
的值 ( )
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
A
解析试题分析:∵函数f(x)是R上的奇函数且是增函数数列,
∴取任何x2>x1,总有f(x2)>f(x1)。
∵函数f(x)是R上的奇函数,∴f(0)=0,
∵函数f(x)是R上的奇函数且是增函数,
∴当x>0,f(0)>0,
当x<0,f(0)<0.
∵数列{an}是等差数列,
a1+a5=2a3, a3>0,∴a1+a5>0,
则f(a1)+f(a5)>0,
∵f(a3)>0,
∴f(a1)+f(a3)+f(a5)恒为正数,故选A。
考点:本题主要考查函数的奇偶性、单调性,等差数列的性质。
点评:中档题,本题综合应用函数奇偶性及单调性,逐步确定得到 满足的条件。有一定综合性,较为典型。
满足的条件。有一定综合性,较为典型。

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
定义在R上的函数f(x)的图像关于x=1对称,且当x≥1时,f(x)=3x-1,则有( )
A.f <f <f < < | B.f <f <f <f <f | C.f <f <f <f <f | D.f <f <f <f <f |
如图,矩形纸板ABCD的顶点A、B分别在正方形边框EOFG的边OE、OF上,当点B在OF边上进行左右运动时,点A随之在OE上进行上下运动.若AB=8,BC=3,运动过程中,则点D到点O距离的最大值为
A. | B.9 | C. | D. |
已知函数 ,则
,则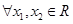 且
且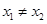 ,有
,有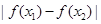 与
与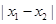 的大小关系为
的大小关系为
A.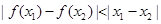 | B.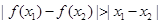 |
C.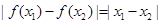 | D.不能确定 |
设函数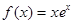 ,则( )
,则( )
A.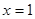 为 为 的极大值点 的极大值点 | B.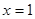 为 为 的极小值点 的极小值点 |
C. 为 为 的极大值点 的极大值点 | D. 为 为 的极小值点 的极小值点 |
已知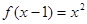 ,则
,则 的表达式为 ( )
的表达式为 ( )
A. | B. |
C.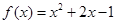 | D. |
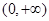 上的单调递减函数
上的单调递减函数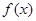 ,若
,若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )