题目内容
已知椭圆C: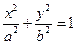 (
( ),其离心率为
),其离心率为 ,两准线之间的距离为
,两准线之间的距离为 。(1)求
。(1)求 之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
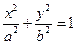 (
( ),其离心率为
),其离心率为 ,两准线之间的距离为
,两准线之间的距离为 。(1)求
。(1)求 之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。(1)a=5,b=3(2)

(1)设c为椭圆的焦半径,则
 。
。
于是有a=5,b=3。
(2) 解法一:设B点坐标为 ,P点坐标为
,P点坐标为 。于是有
。于是有

因为 ,所以有
,所以有
 。 (A1 )
。 (A1 )
又因为ABP为等腰直角三角形,所以有 AB=AP,即
 。 (A2 )
。 (A2 )
由(A1)推出 ,代入(A2),得
,代入(A2),得

从而有 ,即
,即 (不合题意,舍去)或
(不合题意,舍去)或 。
。
代入椭圆方程,即得动点P的轨迹方程

解法二: 设 ,
, ,则以A为圆心,r为半径的圆的参数方程为
,则以A为圆心,r为半径的圆的参数方程为
 。
。
设AB与x轴正方向夹角为 ,B点的参数表示为
,B点的参数表示为
 ,
,
P点的参数表示为
 .
.
从上面两式,得到
 。
。
又由于B点在椭圆上,可得
 。
。
此即为P点的轨迹方程。
 。
。于是有a=5,b=3。
(2) 解法一:设B点坐标为
 ,P点坐标为
,P点坐标为 。于是有
。于是有
因为
 ,所以有
,所以有 。 (A1 )
。 (A1 )又因为ABP为等腰直角三角形,所以有 AB=AP,即
 。 (A2 )
。 (A2 ) 由(A1)推出
 ,代入(A2),得
,代入(A2),得
从而有
 ,即
,即 (不合题意,舍去)或
(不合题意,舍去)或 。
。 代入椭圆方程,即得动点P的轨迹方程

解法二: 设
 ,
, ,则以A为圆心,r为半径的圆的参数方程为
,则以A为圆心,r为半径的圆的参数方程为 。
。设AB与x轴正方向夹角为
 ,B点的参数表示为
,B点的参数表示为 ,
,P点的参数表示为
 .
.从上面两式,得到
 。
。又由于B点在椭圆上,可得
 。
。此即为P点的轨迹方程。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 d,
d, ≤d≤
≤d≤ .
. ·
· =
= ,求向量
,求向量 与
与 与直线
与直线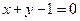 相交于两点
相交于两点 .
. ,且
,且 成等差数列时,求椭圆的方程;
成等差数列时,求椭圆的方程; 的长度
的长度 ;
;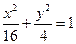 ,过点
,过点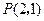 引1条弦,使它在这点平分,求此弦所在直线方程.
引1条弦,使它在这点平分,求此弦所在直线方程.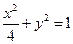 上一点A到左焦点的距离为
上一点A到左焦点的距离为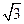 ,则点A到直线
,则点A到直线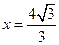 的距离为( )
的距离为( )



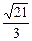 的双曲线过点P(6,6).
的双曲线过点P(6,6). 。
。 ,
, ,则
,则 的轨迹方程是
的轨迹方程是