题目内容
已知向量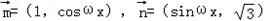 (ω>0),函数
(ω>0),函数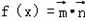 ,且f(x)图象上一个最高点的坐标为
,且f(x)图象上一个最高点的坐标为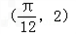 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为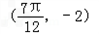 .
.
(1)求f(x)的解析式;
(2)在△ABC中,a,b,c是角A、B、C所对的边,且满足a2+c2﹣b2=ac,求角B的大小以及f(A)的取值范围.
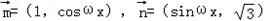 (ω>0),函数
(ω>0),函数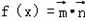 ,且f(x)图象上一个最高点的坐标为
,且f(x)图象上一个最高点的坐标为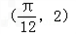 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为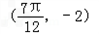 .
.(1)求f(x)的解析式;
(2)在△ABC中,a,b,c是角A、B、C所对的边,且满足a2+c2﹣b2=ac,求角B的大小以及f(A)的取值范围.
解:(1)∵向量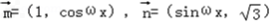
∴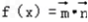 =sinωx+
=sinωx+ cosωx=
cosωx=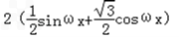 =
=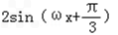 .
.
∵f(x)图象上一个最高点的坐标为 ,
,
与之相邻的一个最低点的坐标为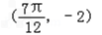 .
.
∴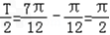 ,∴T=π,
,∴T=π,
于是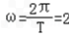 .
.
所以 .
.
(2)∵a2+c2﹣b2=ac,
∴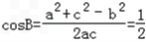
又0<B<π,
∴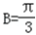 .∴
.∴
∵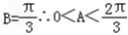 .于是
.于是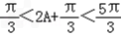 ,
,
∴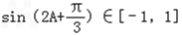 .
.
所以f(A)∈[﹣2,2].
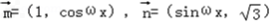
∴
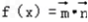 =sinωx+
=sinωx+ cosωx=
cosωx=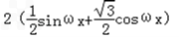 =
=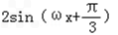 .
.∵f(x)图象上一个最高点的坐标为
 ,
,与之相邻的一个最低点的坐标为
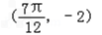 .
.∴
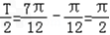 ,∴T=π,
,∴T=π,于是
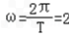 .
.所以
 .
.(2)∵a2+c2﹣b2=ac,
∴
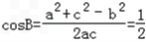
又0<B<π,
∴
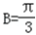 .∴
.∴
∵
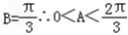 .于是
.于是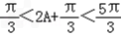 ,
,∴
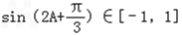 .
.所以f(A)∈[﹣2,2].

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目