题目内容
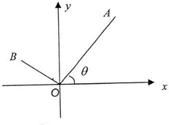
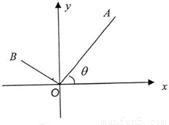
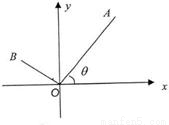
如图，已知A（3，4），点O为坐标原点，点B在第二象限，且|OB|=3，记∠AOx=θ．（1）求sin2θ．
（2）若|AB|=7，求sin∠BOx的值．
【答案】分析：（1）先求sinθ，cosθ，然后求sin2θ．
（2）利用余弦定理求出cos∠BOA，然后求sin∠BOx的值．
解答：解：（Ⅰ）
（2分）
则
（4分）
（Ⅱ）∵|BO|=3，|AO|=5，|AB|=7
∴
∴∠BOA=120°（8分）
sin∠BOx=sin（120°+θ）=sin120°cosθ+cos120°sinθ=
（12分）
点评：本题考查任意角的三角函数的定义，二倍角公式，是基础题．
（2）利用余弦定理求出cos∠BOA，然后求sin∠BOx的值．
解答：解：（Ⅰ）
（2分）则
（4分）（Ⅱ）∵|BO|=3，|AO|=5，|AB|=7
∴
∴∠BOA=120°（8分）
sin∠BOx=sin（120°+θ）=sin120°cosθ+cos120°sinθ=
（12分）点评：本题考查任意角的三角函数的定义，二倍角公式，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
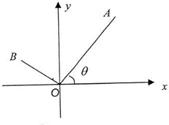如图，已知A（3，4），点O为坐标原点，点B在第二象限，且|OB|=3，记∠AOx=θ．
如图，已知A（3，4），点O为坐标原点，点B在第二象限，且|OB|=3，记∠AOx=θ．
