题目内容
10．设集合A={y|y=x2-4x+5}，集合B={x|x2-1=0}，则A∩B=（ ）| A． | {-1} | B． | {1} | C． | {-1，1，5} | D． | ∅ |
分析 求出A中y的范围确定出A，求出B中方程的解确定出B，找出A与B的交集即可．
解答 解：由A中y=x2-4x+5=x2-4x+4+1=（x-2）2+1≥1，得到A=[1，+∞），
由B中方程解得：x=1或-1，即B={-1，1}，
则A∩B={1}．
故选：B．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
20．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，直线x=a与双曲线的渐近线在第一象限的交点为A，且直线AF与双曲线的一条渐近线关于直线y=b对称，则双曲线的离心率为（ ）
| A． | $\sqrt{5}$ | B． | 3 | C． | 2 | D． | $\sqrt{2}$ |
1．不等式$\frac{1}{x-1}$≤$\frac{1}{{x}^{2}-1}$的解集为（ ）
| A． | （-∞，-1） | B． | [0，1） | C． | （-∞，-1）∪[0，1） | D． | （-1，0]∪（1，+∞） |
15．据《法制晚报》报道，2009年8月15日至8月28日，全国查处酒后驾车和醉酒驾车共28800人，图1是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图，从左到右各直方块表示的人数依次记为A1、A2、…、A8（例如A2表示血液酒精浓度在30～40mg/100ml的人数），图2是对图1中血液酒精浓度在某一范围内的人数进行统计的程序框图．这个程序框图输出的s=（ ）
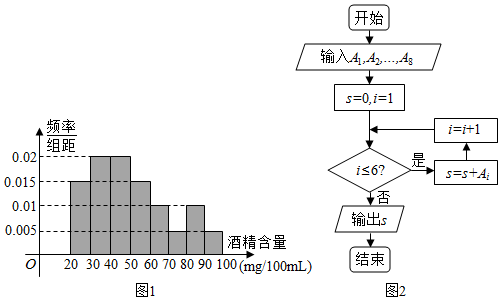
| A． | 24480 | B． | 24380 | C． | 23040 | D． | 23140 |
2．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，O为坐标原点，P是双曲线在第一象限上的点，$\overrightarrow{MO}$=$\overrightarrow{OP}$，直线PF2交双曲线C于另一点N，若|PF1|=2|PF2|，且∠MF2N=120°，则双曲线C的离心率为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\sqrt{7}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |