题目内容
已知点 D 为△ABC 的边 BC 上一点.且 BD=2DC,∠ADB=75°,∠ACB=30°,AD= .
.
(I)求CD的长;
(II)求△ABC的面积.
解:(I)因为∠ADB=75°,∠ACB=30°,所以∠DAC=45°,在△ACD中,AD= ,
,
根据正弦定理有 ,…(4分)
,…(4分)
所以CD=2. …(6分)
(II)由 BD=2DC,可得BD=4. …(7分)
又在△ABD中,∠ADB=75°,sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=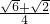 ,…(9分)
,…(9分)
所以 S△ADB=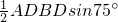 =
= +1,…(12分)
+1,…(12分)
所以 S△ABC= S△ADB=
S△ADB=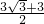 . …(13分)
. …(13分)
分析:(I)先求出∠DAC=45°,根据正弦定理有 ,由此求得CD的值.
,由此求得CD的值.
(II)又在△ABD中,∠ADB=75°,利用两角和的正弦公式求得sin75°=sin(45°+30°)的值,可得S△ADB的值,再由S△ABC= S△ADB 求得结果.
S△ADB 求得结果.
点评:本题主要考查两角和差的正弦公式,正弦定理的应用,属于中档题.
 ,
,根据正弦定理有
 ,…(4分)
,…(4分)所以CD=2. …(6分)
(II)由 BD=2DC,可得BD=4. …(7分)
又在△ABD中,∠ADB=75°,sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=
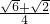 ,…(9分)
,…(9分)所以 S△ADB=
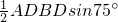 =
= +1,…(12分)
+1,…(12分)所以 S△ABC=
 S△ADB=
S△ADB=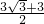 . …(13分)
. …(13分)分析:(I)先求出∠DAC=45°,根据正弦定理有
 ,由此求得CD的值.
,由此求得CD的值.(II)又在△ABD中,∠ADB=75°,利用两角和的正弦公式求得sin75°=sin(45°+30°)的值,可得S△ADB的值,再由S△ABC=
 S△ADB 求得结果.
S△ADB 求得结果.点评:本题主要考查两角和差的正弦公式,正弦定理的应用,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2013•福建)如图,在△ABC中,已知点D在BC边上,AD⊥AC,
(2013•福建)如图,在△ABC中,已知点D在BC边上,AD⊥AC, 如图,已知点P为椭圆
如图,已知点P为椭圆