题目内容
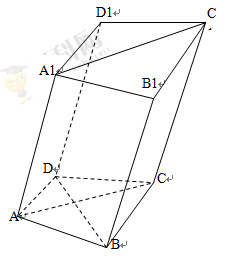
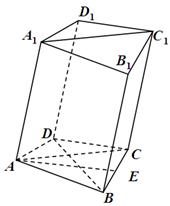
如图,在四棱柱 中,已知平面
中,已知平面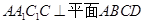 ,且
,且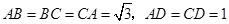 .
.
(1)求证: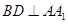 ;
;
(2)在棱BC上取一点E,使得 ∥平面
∥平面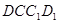 ,求
,求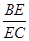 的值.
的值.
【答案】
(1)证明参考解析;(2)
【解析】
试题分析:(1)由于AB=CB,AD=CD,BD=BD.可得三角形ABD全等于三角形CBD.所以这两个三角形关于直线BD对称.所以可得 .再由面面垂直即可得直线BD垂直于平面
.再由面面垂直即可得直线BD垂直于平面 .从而可得
.从而可得 .
.
(2)由于AC= .AD=CD=1.所以可得角ACD等于300.又因为角ACB等于600.所以可得角DCB为直角.所以取BC边上的中点即为所求的点.本题考查的知识点是面面垂直线面垂直即线面平行.以及一个开放性的问题.
.AD=CD=1.所以可得角ACD等于300.又因为角ACB等于600.所以可得角DCB为直角.所以取BC边上的中点即为所求的点.本题考查的知识点是面面垂直线面垂直即线面平行.以及一个开放性的问题.
试题解析:证明:(1)在四边形ABCD中,因为BA=BC,DA=DC,所以 .
.
平面 ,且
,且
所以 .
.
(2)点E为BC中点,即 ,
,
下面给予证明:在三角形ABC中,因为AB=AC,却E为BC中点,所以 ,
,
又在四边形ABCD中,AB=BC=CA= ,DA=DC=1,所以
,DA=DC=1,所以 ,
,
所以  ,即平面ABCD中有,
,即平面ABCD中有, .
.
因为 平面
平面 .AE
.AE 平面
平面 .
.
所以 AE∥平面 .
.
考点:1.面面平行.2.线线垂直.3.线面平行.4.开放性的题目.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=
如图,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=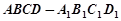 中,已知平面
中,已知平面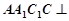 平面
平面 且
且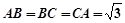 ,
,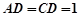 .
.
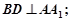
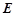 为棱
为棱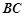 的中点,求证:
的中点,求证: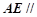 平面
平面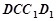 .
. (1)设
(1)设 (1)设
(1)设