题目内容
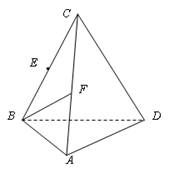
(本小题11分)如图,在四棱锥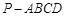 中,
中,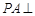 平面
平面 ,
,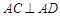 ,
,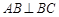 ,
, ,
,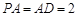 ,
,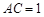 .
.
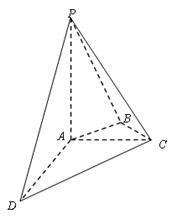
(1)证明: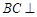 平面
平面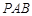
(2)求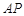 和平面
和平面 所成角的正弦值
所成角的正弦值
(3)求二面角 的正切值;
的正切值;
【答案】
(1)见解析;(2)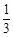 ;(3)
;(3) 。
。
【解析】
试题分析:(1) 平面
平面 ,所以
,所以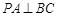 ,又
,又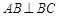
所以 平面
平面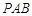 ……………… 2分
……………… 2分
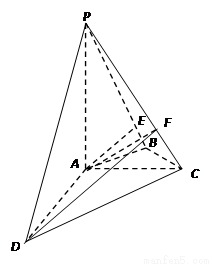
(2)如图,作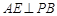 ,交
,交 于点
于点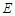 ,
,
 平面
平面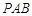 ,
, 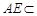 平面
平面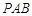 所以
所以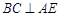
又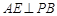 ,所以
,所以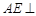 平面
平面
所以 是
是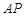 和平面
和平面 所成角………………4分
所成角………………4分
 中,
中,
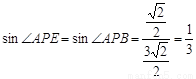 ……………………6分
……………………6分
所以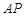 和平面
和平面 所成角的正弦为
所成角的正弦为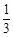 ……………… 7分
……………… 7分
(3)作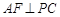 交
交 于点
于点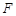 ,连接
,连接
 平面
平面 ,所以
,所以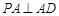 ,又
,又 ,所以
,所以 平面
平面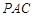 ,所以
,所以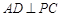
又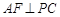 ,所以
,所以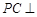 平面
平面 ,所以
,所以 ,
,
所以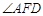 是二面角
是二面角 的平面角。……………… 9分
的平面角。……………… 9分
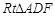 中,
中,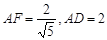 ,
,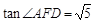
二面角 的正切值为
的正切值为 …………………… 11分
…………………… 11分
(用向量法酌情给分)
考点:线面垂直的性质定理;线面垂直的判定定理;面面垂直项性质定理;直线与平面所成的角;二面角。
点评:本题主要考查的知识点是二面角的平面角及求法,直线与平面垂直的判定。解决这类问题的常用方法有:综合法和向量法。本题用的是综合法,当然也可以用向量法。

练习册系列答案
相关题目
 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值 如图,在ΔOAB中,已知
如图,在ΔOAB中,已知 (1)若
(1)若