题目内容
![]()
![]() 中,
中,![]()
![]() 分别是角
分别是角![]()
![]() 的对边,
的对边,![]()
![]() ,
,![]()
![]() ,且
,且![]()
![]()
(1)求角![]()
![]() 的大小;
的大小;
(2)设![]()
![]() ,且
,且![]()
![]() 的最小正周期为
的最小正周期为![]()
![]() ,求
,求![]()
![]() 在
在![]()
![]() 上的最大值和最小值,及相应的
上的最大值和最小值,及相应的![]()
![]() 的值。
的值。
(1)由![]() ∥
∥![]() 得
得![]() ,
,![]()
![]()
得到![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]()
又![]() ,又
,又![]() ,
,![]()
(2) (2)由题知f(x)=cos(ωx-![]() )+sinωx
)+sinωx
=![]() cosωx+
cosωx+![]() sinωx=
sinωx=![]() sin(ωx+
sin(ωx+![]() ),
),
由已知得![]() =π,∴ω=2,f(x)=
=π,∴ω=2,f(x)=![]() sin(2x+
sin(2x+![]() ),
),
当x∈[0,![]() ]时,(2x+
]时,(2x+![]() )∈[
)∈[![]() ,
,![]() ],
],
sin(2x+![]() )∈[-
)∈[-![]() ,1].
,1].
因此,当2x+![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取得最大值
时,f(x)取得最大值![]() .
.
当2x+![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取得最小值-
时,f(x)取得最小值-![]() .
.

练习册系列答案
相关题目
 ,设函数
,设函数 ,(Ⅰ)求函数
,(Ⅰ)求函数 的表达式;(Ⅱ)在
的表达式;(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若
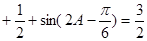 ,
,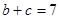 ,
, ,求边
,求边 的长.
的长. ,其中向量
,其中向量
 ,
,
 .
. 的最小正周期;
的最小正周期; 中,
中, 分别是角
分别是角 的对边,
的对边, ,
,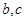 的长.
的长.