题目内容
如图,已知四棱锥 ,底面
,底面 为菱形,
为菱形, 平面
平面 ,
,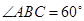 ,
,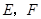 分别是
分别是 的中点.
的中点.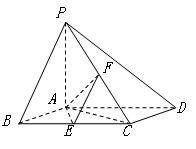
(1)证明: ;
;
(2)若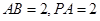 ,求二面角
,求二面角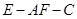 的余弦值.
的余弦值.
(1)证明:见解析;(2)二面角的余弦值为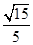 .
.
解析试题分析:(1)首先可得  为正三角形.
为正三角形.
根据 为
为 的中点,得到
的中点,得到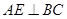 .进一步有
.进一步有 .
.
由 平面
平面 ,证得
,证得 .
.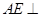 平面
平面 .即得
.即得 .
.
(2)思路一:利用几何方法.遵循“一作,二证,三计算”,过 作
作 于
于 ,有
,有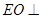 平面
平面 ,
,
过 作
作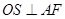 于
于 ,连接
,连接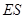 ,
,
即得 为二面角
为二面角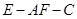 的平面角,
的平面角,
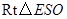 中,
中,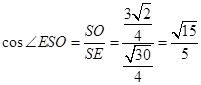 .
.思路二:利用“向量法”:由(1)知
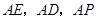 两两垂直,以
两两垂直,以 为坐标原点,建立如图所示的空间直角坐标系,
为坐标原点,建立如图所示的空间直角坐标系,确定平面
 的一法向量及
的一法向量及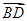 为平面
为平面 的一法向量.
的一法向量.计算
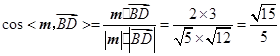 .
.试题解析:(1)证明:由四边形
 为菱形,
为菱形,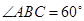 ,可得
,可得 为正三角形.
为正三角形.因为
 为
为 的中点,所以
的中点,所以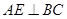 .
.又
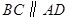 ,因此
,因此 .
.因为
 平面
平面 ,
, 平面
平面 ,所以
,所以 .
.而
 平面
平面 ,
, 平面
平面 且
且 ,
,所以
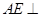 平面
平面 .又
.又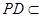 平面
平面 ,
,所以
 . (7分)
. (7分)(2)解法一:因为
 平面
平面 ,
, 平面
平面 ,
,所以平面
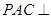 平面
平面 .
.过
 作
作 于
于 ,则
,则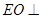 平面
平面 ,
,过
 作
作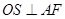 于
于 ,连接
,连接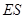 ,
,
|
 为二面角
为二面角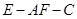 的平面角,
的平面角,
在
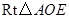 中,
中,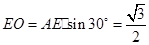 ,
, ,
,又
 是
是 的中点,在
的中点,在 中,
中, ,
,又
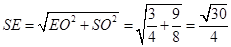 , 在
, 在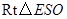 中,
中,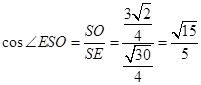 ,
,即所求二面角的余弦值为
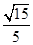 . (14分)
. (14分)解法二:由(1)知
 两两垂直,以
两两垂直,以 为坐标原点,建立如图所示的空间直角坐标系,又
为坐标原点,建立如图所示的空间直角坐标系,又 分别为
分别为 的中点,所以
的中点,所以
 ,
,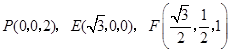 ,
,所以
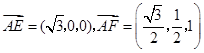 .
.设平面
 的一法向量为
的一法向量为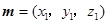 ,
,则
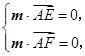 因此
因此
取
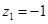 ,则
,则 ,
,因为
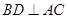 ,
,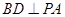 ,
,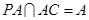 ,
,所以
 平面
平面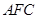 ,
,故
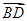 为平面
为平面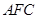 的一法向量.
的一法向量.又
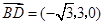 ,
,所以
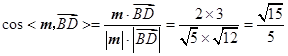 .
.因为二面角
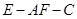 为锐角,
为锐角,所以所求二面角的余弦值为
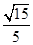 .
.考点:1.垂直关系;2.空间的角;3.空间向量方法.

练习册系列答案
相关题目
已知 是虚数单位,
是虚数单位, 和
和 都是实数,且
都是实数,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
直线 经过第一、第二和第四象限,则
经过第一、第二和第四象限,则 应满足( )
应满足( )
A. | B. | C. | D. |
已知直线 与直线
与直线 平行,则它们之间的距离是( )
平行,则它们之间的距离是( )
| A.1 | B.2 | C. | D.4 |
若函数 的图象在点
的图象在点 处的切线
处的切线 被圆
被圆 所截得的弦长是
所截得的弦长是 ,则
,则
A. | B. | C. | D. |
 与
与 的夹角为
的夹角为 ,若(
,若( )
) (
( ),则
),则 .
. 的通项公式为
的通项公式为 ,对于任意自然数
,对于任意自然数 都是递增数列,
都是递增数列, 的取值范围为 .
的取值范围为 . ,则关于x的不等式f(x2)>f(3-2x)的解集是_______________.
,则关于x的不等式f(x2)>f(3-2x)的解集是_______________. ,沿着较短的对角线
,沿着较短的对角线 对折,使得
对折,使得 ,
, 为
为 的中点.若P为AC上的点,且满足
的中点.若P为AC上的点,且满足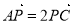 。
。
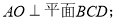
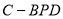 的体积;
的体积; 的余弦值.
的余弦值.