题目内容
设双曲线C：
的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q。
（Ⅰ）若直线m与x轴正半轴的交点为T，且
，求点T的坐标；
（Ⅱ）求直线A1P与直线A2Q的交点M的轨迹E的方程；
（Ⅲ）过点F（1，0）作直线l与（Ⅱ）中的轨迹E交于不同的两点A、B，设
，若
（T为（Ⅰ）中的点）的取值范围。
（Ⅰ）点T的坐标为（2，0）
（Ⅱ）
（Ⅲ）
解析:
（Ⅰ）由题，得
，设
则
由
…………①
又
在双曲线上，则
…………②
联立①、②，解得 
由题意， 
∴点T的坐标为（2，0） …………3分
（Ⅱ）设直线A1P与直线A2Q的交点M的坐标为（x，y）
由A1、P、M三点共线，得
…………③ …………1分
由A2、Q、M三点共线，得
…………④ …………1分
联立③、④，解得 
…………1分
∵在双曲线上，
∴
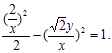
∴轨迹E的方程为
…………1分
（Ⅲ）容易验证直线l的斜率不为0。
故可设直线l的方程为 
中，得
设 
则由根与系数的关系，得
……⑤
……⑥ …………2分
∵
∴有
将⑤式平方除以⑥式，得
…………1分
由
…………1分
∵
又
故
令
∴
，即 
∴
而 
， ∴
∴
练习册系列答案
相关题目
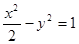的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点
。
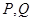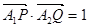，求点T的坐标；
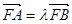，若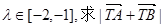
（T为（1）中的点）的取值范围。
=1的左、右焦点分别为F1、F2，点P是双曲线位于第一象限内的一个点，且满足
·
=0,则△PF1F2的内切圆的方程为
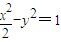的左、右顶点分别为A1、A2，垂直于x轴的直线l与双曲线C交于不同的两点P、Q．若直线l与x轴正半轴的交点为M，且
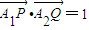，则点M的坐标为（ ）
，0）
，0）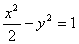
的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q。
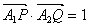，求点T的坐标；