题目内容
(2011•东城区一模)已知椭圆
+
=1(a>b>0)的离心率为
,且椭圆上的点到两个焦点的距离和为2
.斜率为k(k≠0)的直线l过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴相交于点M(0,m).
(Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)试用m表示△MPQ的面积,并求面积的最大值.
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)试用m表示△MPQ的面积,并求面积的最大值.
分析:(Ⅰ) 根据椭圆的定义,椭圆上的点到两个焦点的距离之和等于长轴长,就可求出a,再根据椭圆的离心率e=
,就可求出c值,再结合椭圆中a,b,c的关系式求出b值,就可得到椭圆方程.
(Ⅱ)因为直线l斜率为k(k≠0)且过椭圆的上焦点,就可得到直线l的方程为y=kx+1,与椭圆方程联立,解得P,Q两点的横坐标之和,纵坐标之和,均用含k的式子表示,线段PQ的垂直平分线斜率等于直线l斜率的负倒数且过线段PQ的中点,就可以k为参数求出垂直平分线的点斜式方程,令x=0,解出M点的坐标,把m用含k的式子表示,根据k的范围求出m的范围.
(Ⅲ)y轴把△PQM分成了两个三角形,△PMF1和△QMF1所以△PQM的面积就是△PMF1和△QMF1的面积之和.△PMF1和△QMF1都可看做以MF1为底,高分别为P点和Q点的横坐标的绝对值,利用(Ⅱ)中得到的x1+x2,x1x2的值,就可把△PQM的面积用含m的式子表示,再利用导数求出最大值即可.
| c |
| a |
(Ⅱ)因为直线l斜率为k(k≠0)且过椭圆的上焦点,就可得到直线l的方程为y=kx+1,与椭圆方程联立,解得P,Q两点的横坐标之和,纵坐标之和,均用含k的式子表示,线段PQ的垂直平分线斜率等于直线l斜率的负倒数且过线段PQ的中点,就可以k为参数求出垂直平分线的点斜式方程,令x=0,解出M点的坐标,把m用含k的式子表示,根据k的范围求出m的范围.
(Ⅲ)y轴把△PQM分成了两个三角形,△PMF1和△QMF1所以△PQM的面积就是△PMF1和△QMF1的面积之和.△PMF1和△QMF1都可看做以MF1为底,高分别为P点和Q点的横坐标的绝对值,利用(Ⅱ)中得到的x1+x2,x1x2的值,就可把△PQM的面积用含m的式子表示,再利用导数求出最大值即可.
解答:解:(Ⅰ)椭圆上的点到两个焦点的距离和为2
,即2a=2
,∴a=
椭圆
+
=1(a>b>0)的离心率为
,即e=
∵e=
,∴
=
,
∴c=1
又∵a2=b2+c2,∴b=1.
又斜率为k(k≠0)的直线l过椭圆的上焦点,即椭圆的焦点在Y轴上
∴椭圆方程为
+x2=1.
(Ⅱ)设直线l的方程为y=kx+1,由
可得(k2+2)x2+2kx-1=0.
设P(x1,y1),Q(x2,y2),则△=8k2+8>0
x1+x2=
,x1x2=-
.
y1+y2=k(x1+x2)+2=
.
设线段PQ中点为N,则点N的坐标为(
,
),
∵M(0,m),∴直线MN的斜率kMN=
∵直线MN为PQ的垂直平分线,∴kMN•k=-1,
可得
•k=-1.即m=
,
又k≠0,∴k2+2>2,
∴0<
<
,即0<m<
.
(Ⅲ)设椭圆上焦点为F,
∵y轴把△PQM分成了△PMF和△QMF,
∴S△MPQ=S△PMF +S△QMF =
|FM||x1|+
|FM||x2|=
|FM|(|x1|+|x2|)
∵P,Q在y轴两侧,∴|x1|+|x2|=||(x1-x2)
∴S△MPQ=
•|FM|•|x1-x2|,
∵|x1-x2|=
=
,
由m=
,可得k2+2=
.
∴|x1-x2|=
=
.
又∵|FM|=1-m,∴S△MPQ=
(1-m)
=
.
∴△MPQ的面积为
(0<m<
).
设f(m)=m(1-m)3,则f'(m)=(1-m)2(1-4m).
可知f(m)在区间(0,
]单调递增,在区间(
,
)单调递减.
∴f(m)=m(1-m)3有最大值f(
)=
.此时∴△MPQ的面积为
×
=
∴△MPQ的面积有最大值
.
| 2 |
| 2 |
| 2 |
椭圆
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
∵e=
| c |
| a |
| c |
| a |
| ||
| 2 |
∴c=1
又∵a2=b2+c2,∴b=1.
又斜率为k(k≠0)的直线l过椭圆的上焦点,即椭圆的焦点在Y轴上
∴椭圆方程为
| y2 |
| 2 |
(Ⅱ)设直线l的方程为y=kx+1,由
|
设P(x1,y1),Q(x2,y2),则△=8k2+8>0
x1+x2=
| -2k |
| k2+2 |
| 1 |
| k2+2 |
y1+y2=k(x1+x2)+2=
| 4 |
| k2+2 |
设线段PQ中点为N,则点N的坐标为(
| -k |
| k2+2 |
| 2 |
| k2+2 |
∵M(0,m),∴直线MN的斜率kMN=
m-
| ||
|
∵直线MN为PQ的垂直平分线,∴kMN•k=-1,
可得
m-
| ||
|
| 1 |
| k2+2 |
又k≠0,∴k2+2>2,
∴0<
| 1 |
| k2+2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ)设椭圆上焦点为F,
∵y轴把△PQM分成了△PMF和△QMF,
∴S△MPQ=S△PMF +S△QMF =
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵P,Q在y轴两侧,∴|x1|+|x2|=||(x1-x2)
∴S△MPQ=
| 1 |
| 2 |
∵|x1-x2|=
| (x1+x2)2-4x1x2 |
|
由m=
| 1 |
| k2+2 |
| 1 |
| m |
∴|x1-x2|=
|
| 8m(1-m) |
又∵|FM|=1-m,∴S△MPQ=
| 1 |
| 2 |
| 8m(1-m) |
| 2m(1-m)3 |
∴△MPQ的面积为
| 2 |
| m(1-m)3 |
| 1 |
| 2 |
设f(m)=m(1-m)3,则f'(m)=(1-m)2(1-4m).
可知f(m)在区间(0,
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴f(m)=m(1-m)3有最大值f(
| 1 |
| 4 |
| 27 |
| 256 |
| 2 |
|
3
| ||
| 16 |
∴△MPQ的面积有最大值
3
| ||
| 16 |
点评:本题(Ⅰ)考查了椭圆定义的应用和椭圆性质的应用求椭圆方程,(Ⅱ)考查了直线与椭圆位置关系的判断,以及韦达定理的应用,(Ⅲ)考查了应用导数求最值.本题综合性强,须认真分析,正确作答.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
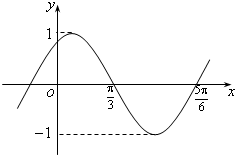 (2011•东城区一模)已知函数y=sin(ωx+φ)
(2011•东城区一模)已知函数y=sin(ωx+φ)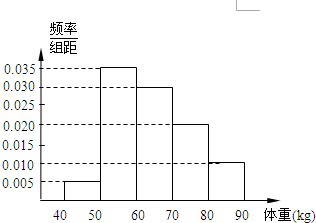 (2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为
(2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为