题目内容
已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
A
解析试题分析:由 ,根据三角函数的和角公式可知,
,根据三角函数的和角公式可知, ①.因为
①.因为 ,所以
,所以 ,所以
,所以 ,由三角函数的和角公式得,
,由三角函数的和角公式得, ②.由①②解得
②.由①②解得 ,
,
 ,
, .
.
考点:1.三角函数的和角公式;2.同角三角函数的基本关系

练习册系列答案
相关题目
已知函数 ,下列命题是真命题的为( )
,下列命题是真命题的为( )
A.若 ,则 ,则 . . |
B.函数在区间 上是增函数. 上是增函数. |
C.直线 是函数的一条对称轴. 是函数的一条对称轴. |
D.函数图象可由 向右平移 向右平移 个单位得到. 个单位得到. |
已知 是第二象限,且
是第二象限,且 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
若函数 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,则
上单调递减,则 =( )
=( )
| A.3 | B.2 | C. | D. |
已知 是单位向量且
是单位向量且 ,则
,则 的最大值为( )
的最大值为( )
A. | B.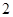 | C. | D. |
函数 是 ( )
是 ( )
A.最小正周期为 的偶函数 的偶函数 | B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 | D.最小正周期为 的奇函数 的奇函数 |
 ;(2)图像关于直线
;(2)图像关于直线 对称;(3)在
对称;(3)在 上是增函数”的一个函数是( )
上是增函数”的一个函数是( )



 =a1a4-a2a3;将函数f(x)=
=a1a4-a2a3;将函数f(x)= 的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )
的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )



 在圆
在圆 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间 时,点
时,点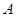 的坐标是
的坐标是 ,则当
,则当 时,动点
时,动点 关于
关于 (单位:秒)的函数的单调递增区间是( )
(单位:秒)的函数的单调递增区间是( )

