题目内容
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() .
.
(1)求证:![]() ;
;
(2)若对于任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若存在![]() ,使
,使![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;
(2)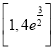 ;
;
(3)![]() 或
或![]() .
.
【解析】
(1)对利用导数研究函数的单调性及最小值,进而证明不等式;
(2)由题意得![]() ,对
,对![]() 分成
分成![]() 三种情况讨论,进而利用参变分离,构造新函数,利用导数研究新函数的最值,从而得到
三种情况讨论,进而利用参变分离,构造新函数,利用导数研究新函数的最值,从而得到![]() 的取值范围;
的取值范围;
(3)设![]() ,题设等价于函数
,题设等价于函数![]() 有零点时的
有零点时的![]() 的取值范围,先对函数进行求导得
的取值范围,先对函数进行求导得![]() ,再对
,再对![]() 分成
分成![]() 三种情况进行研究函数的零点.
三种情况进行研究函数的零点.
解:(1)令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 处取得最小值,因为
处取得最小值,因为![]() ,
,
所以![]() .
.
(2)由题意,得![]() ,
,
当![]() ,不等式显然成立,此时
,不等式显然成立,此时![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
记![]() ,
,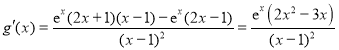 ,
,
∴![]() 在区间
在区间![]() 和
和![]() 上为增函数,
上为增函数,![]() 和
和![]() 上为减函数.
上为减函数.
∴当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
综上所述![]() 的取值范围为
的取值范围为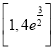 .
.
(3)设![]() ,题设等价于函数
,题设等价于函数![]() 有零点时的
有零点时的![]() 的取值范围.
的取值范围.
![]()
当![]() ,
,![]() ,
,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 单调递增,
单调递增,
![]() ,
,
若![]() ,则
,则![]() ,
,
只需![]() ,则
,则![]() ,则
,则![]() ,
,
所以![]() 有零点.
有零点.
当![]() 时,
时,![]() ,对
,对![]() 恒成立,
恒成立,
所以![]() 无零点,不成立.
无零点,不成立.
当![]() 时,
时,![]() ,得
,得![]() ,
,
则![]() 时
时![]() ,所以
,所以![]() 在
在![]() 单调递减;
单调递减;
![]() 时
时![]() ,所以
,所以![]() 在在
在在![]() 单调递增,
单调递增,
所以![]() ,
,
①![]() 时,
时,![]() ,
,![]() ,
,
又![]() ,
,
所以![]() 有零点;
有零点;
②![]() 时,
时,![]() ,
,![]()
所以![]() 有零点;
有零点;
③![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 无零点,不成立.
无零点,不成立.
综上,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.

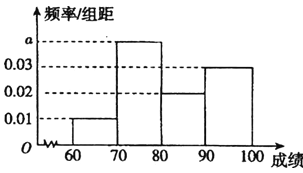
【题目】某工厂生产一批零件,为了解这批零件的质量状况,检验员从这批产品中随机抽取了100件作为样本进行检测,将它们的重量(单位:g)作为质量指标值,由检测结果得到如下频率分布表和频率分布直方图.
分组 | 频数 | 频率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合计 | 100 | 1 |
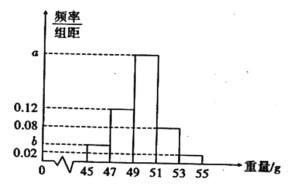
(1)求图中![]() ,
,![]() 的值;
的值;
(2)根据质量标准规定:零件重量小于47或大于53为不合格品,重量在区间![]() 和
和![]() 内为合格品,重量在区间
内为合格品,重量在区间![]() 内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该批零件重量的概率分布.若这批零件共400件,现有两种销售方案:
内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该批零件重量的概率分布.若这批零件共400件,现有两种销售方案:
方案一:对剩余零件不再进行检测,回收处理这100件样本中的不合格品,余下所有零件均按150元/件售出;
方案二:继续对剩余零件的重量进行逐一检测,回收处理所有不合格品,合格品按150元/件售出,优质品按200元/件售出.
仅从获得利润大的角度考虑,该生产商应选择哪种方案?请说明理由.