题目内容
在△ABC中,内角A、B、C的对边长分别为a、b、c,已知函数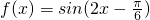 满足:对于任意x∈R,f(x)≤f(A))恒成立.
满足:对于任意x∈R,f(x)≤f(A))恒成立.
(1)求角A的大小;
(2)若 ,求BC边上的中线AM长的取值范围.
,求BC边上的中线AM长的取值范围.
解:(1)由题意可得f(A)为函数f(x)的最大值,即 =1,∴A=
=1,∴A= .
.
(2)若 ,则BM=
,则BM= ,△ABM中,由余弦定理可得 c2=
,△ABM中,由余弦定理可得 c2= +AM2-2×
+AM2-2× cos∠AMB ①.
cos∠AMB ①.
在△ACM中,由余弦定理可得 b2 = +AM2-2×
+AM2-2× cos∠AMC=
cos∠AMC= +AM2 +2×
+AM2 +2× cos∠AMB ②.
cos∠AMB ②.
把①、②相加可得AM2 = -
- .
.
△ABC中,再由余弦定理可得 3=b2+c2-2bc•cosA=b2+c2-bc,
故有 b2+c2 =3+bc>3,且 b2+c2-bc=3≥b2+c2- ,
,
化简可得3<b2+c2≤6,∴AM∈( ,
, ].
].
分析:(1)由题意可得f(A)为函数f(x)的最大值,即 =1,由此求得角A 的值.
=1,由此求得角A 的值.
(2)利用余弦定理可得AM2=- +
+ ,3=b2+c2-bc,从而得到 3<b2+c2≤6,由此求得BC边上的中线AM长的
,3=b2+c2-bc,从而得到 3<b2+c2≤6,由此求得BC边上的中线AM长的
取值范围.
点评:本题主要考查余弦定理,求三角函数的最值,以及不等式性质的应用,属于中档题.
 =1,∴A=
=1,∴A= .
.(2)若
 ,则BM=
,则BM= ,△ABM中,由余弦定理可得 c2=
,△ABM中,由余弦定理可得 c2= +AM2-2×
+AM2-2× cos∠AMB ①.
cos∠AMB ①.在△ACM中,由余弦定理可得 b2 =
 +AM2-2×
+AM2-2× cos∠AMC=
cos∠AMC= +AM2 +2×
+AM2 +2× cos∠AMB ②.
cos∠AMB ②.把①、②相加可得AM2 =
 -
- .
.△ABC中,再由余弦定理可得 3=b2+c2-2bc•cosA=b2+c2-bc,
故有 b2+c2 =3+bc>3,且 b2+c2-bc=3≥b2+c2-
 ,
,化简可得3<b2+c2≤6,∴AM∈(
 ,
, ].
].分析:(1)由题意可得f(A)为函数f(x)的最大值,即
 =1,由此求得角A 的值.
=1,由此求得角A 的值.(2)利用余弦定理可得AM2=-
 +
+ ,3=b2+c2-bc,从而得到 3<b2+c2≤6,由此求得BC边上的中线AM长的
,3=b2+c2-bc,从而得到 3<b2+c2≤6,由此求得BC边上的中线AM长的取值范围.
点评:本题主要考查余弦定理,求三角函数的最值,以及不等式性质的应用,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目