题目内容
已知函数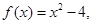
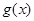 是定义在
是定义在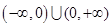 上的奇函数,当
上的奇函数,当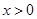 时,
时,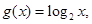 则函数
则函数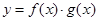 的大致图象为
的大致图象为
D
解析试题分析:因为函数f(x)=4-x2,是定义在R上偶函数,g(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,故函数y=f(x)•g(x)为奇函数,其图象关于原点对称,故A,C不正确,又因为函数f(x)=4-x2,当x>0时,g(x)=log2x,故当0<x<1时,y=f(x)•g(x)>0;当1<x<2时,y=f(x)•g(x)<0;当x>2时,y=f(x)•g(x)>0;故B不正确,故选B
考点:函数的图像;函数的奇偶性。
点评:在判断函数的图象时,分析函数的定义域、单调性、奇偶性、特殊点或者特殊值是最常用的方法.

练习册系列答案
相关题目
函数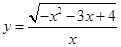 的定义域为 ( )
的定义域为 ( )
A.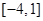 | B.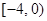 | C.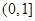 | D.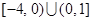 |
函数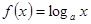 ,在
,在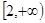 上恒有
上恒有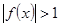 ,则实数
,则实数 的范围是( )
的范围是( )
A.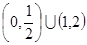 | B. | C.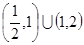 | D.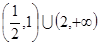 |
若函数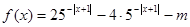 有实数零点,则实数
有实数零点,则实数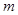 的取值范围是( )
的取值范围是( )
A.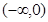 | B.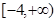 | C.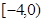 | D.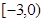 |
已知函数
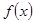 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, ,那么函数
,那么函数
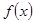 的零点个数为( )
的零点个数为( )
| A.一定是2 | B.一定是3 | C.可能是2也可能是3 | D.可能是0 |
如果奇函数 在区间[2,6]上是增函数,且最小值为4,则
在区间[2,6]上是增函数,且最小值为4,则 在[-6,-2]上是( )
在[-6,-2]上是( )
| A.最大值为-4的增函数 | B.最小值为-4的增函数 |
| C.最小值为-4的减函数 | D.最大值为-4的减函数 |
已知函数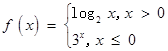 , 则
, 则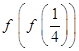 的值是
的值是
A.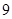 | B. | C.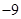 | D.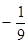 |
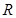 上的函数
上的函数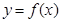 满足
满足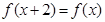 ,当
,当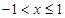 时,
时,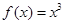 ,若函数
,若函数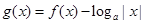 至少有6个零点,则
至少有6个零点,则 的取值范围是 ( )
的取值范围是 ( )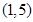
 满足
满足 ,且x∈[-1,1]时,
,且x∈[-1,1]时,  则函数h(x)=f(x)一g(x)在区间[-5,5]内的与x轴交点的个数为
则函数h(x)=f(x)一g(x)在区间[-5,5]内的与x轴交点的个数为