Question

已知数列{a_n}中，a₁=2,S_n为其前n项和，且2a_n,,na_n(n∈N^*)成等差数列.设b_n=,记数列{b_n}的前n项和为T_n.

(1)求数列{a_n}的通项公式.

(2)设=p,试比较与2ⁿ的大小，并证明你的结论.

Answer 1

解:(1)依题意得，2·=2a_n+na_n，即3S_n=(2+n)a_n(n∈N^*)，

∴3S_n-1=(1+n)a _n-1 (n≥2),以上两式相减，得

3（S_n-S _n-1）=(2+n)a_n-(1+n)a _n-1，整理得3a_n=（2+n）a_n-（1+n）a _n-1,

∴.

由此得a_n=a₁·

=a₁·.

又a₁=2,∴a_n=n(n+1)(n∈N^*).

(2)T_n=b₁+b₂+…+b_n=

∴==1,即p=1,则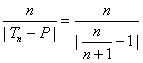=n(n+1),

∴a_n.

当n=1时，a₁=1(1+1)=2,∴a₁=2¹;

当n=2,3,4时，则a₂=2(2+1)=6,

∴a₂＞2²,

a₃=3(3+1)=12,

∴a₃＞2³,a₄=4(4+1)=20,∴a₄＞2⁴;

当n≥5时，猜想a_n＜2ⁿ.

证法如下：∵2ⁿ=(1+1)ⁿ=+

=n²+n+2＞n²+n=n(n+1)=a_n,

∴当n≥5时，a_n＜2ⁿ.

综上所述，当n=1时，＞2ⁿ;

当n=2,3,4时，＞2ⁿ;

n≥5时，＜2ⁿ.