题目内容
15.a>0,c>0是方程ax2+y2=c表示椭圆的( )| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 由a>0,c>0时方程ax2+y2=c不一定表示椭圆,判断充分性不成立;
由方程ax2+y2=c表示椭圆时a>0,c>0成立,判断必要性成立.
解答 解:a>0,c>0时,方程ax2+y2=c不一定表示椭圆,
如a=c=1时,方程表示圆,充分性不成立;
方程ax2+y2=c表示椭圆时,a>0,c>0且a≠1,c≠1,必要性成立;
所以a>0,c>0是方程ax2+y2=c表示椭圆的必要不充分条件.
故选:C.
点评 本题考查了椭圆的定义与性质、充分与必要条件的判断问题.是基础知识的理解和应用问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.有算法语句如下,其运算的结果是( )


| A. | 12 | B. | 3 | C. | 4 | D. | $\frac{275}{72}$ |
20.△ABC的斜二测直观图△A′B′C′如图所示,则△ABC的面积为( )
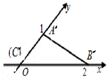

| A. | 1 | B. | 2 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
4.椭圆$\frac{x^2}{4}+{y^2}$=1上的点P到上顶点距离的最大值为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | 不存在最大值 |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.