题目内容
已知函数:![]()
(1)当![]() 的定义域为
的定义域为![]() 时,求证:
时,求证:![]() 的值域为;[0,1];
的值域为;[0,1];
(2)设函数![]() ,求
,求![]() 的最小值.
的最小值.
(1)证明:
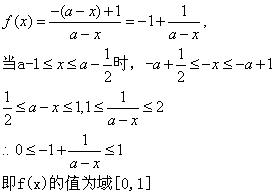
(2)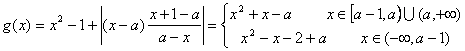
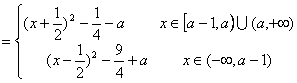
①若![]() 且
且![]() ,则:
,则:
当![]() 时,
时,![]()
当![]() 时,
时,![]()
若![]() 且
且![]() ,则函数的最小值为
,则函数的最小值为![]()
②若![]() ,则:
,则:
当![]() 时,
时,![]()
当![]() 时,
时,![]()
若![]() ,则函数的最小值为
,则函数的最小值为![]()
③若![]() ,则:
,则:
当![]() 时,
时,![]()
当![]() 时,
时,![]()
若![]() ,则函数的最小值为
,则函数的最小值为![]()
综上可得:当![]() 且
且![]() 时,g(x)的最小值为
时,g(x)的最小值为![]() ;
;
当![]() 时,g(x)的最小值为
时,g(x)的最小值为![]() ;
;
当![]() 时,g(x)的最小值为
时,g(x)的最小值为![]() ;
;
当![]() 时,g(x)不存在最小值
时,g(x)不存在最小值

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 ,
,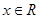 .
.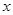 为何值时,
为何值时,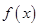 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
,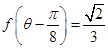 ,求
,求 的值.
的值.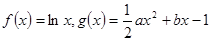 ,
, 且
且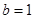 时,证明:对
时,证明:对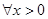 ,
,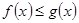 ;
;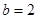 ,且
,且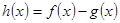 存在单调递减区间,求
存在单调递减区间,求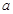 的取值范围;
的取值范围;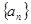 ,若存在常数
,若存在常数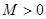 ,
,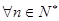 ,都有
,都有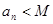 ,则称数列
,则称数列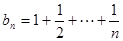 ,试判断数列
,试判断数列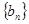 是否有上界.
是否有上界.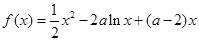 ,
,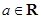 .
.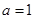 时,求函数
时,求函数 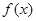 的最小值;
的最小值; 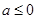 时,讨论函数
时,讨论函数 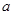 ,对任意的
,对任意的
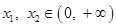 ,且
,且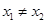 ,有
,有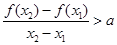 ,恒成立,若存在求出
,恒成立,若存在求出