题目内容
已知椭圆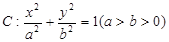 经过点
经过点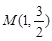 ,其离心率为
,其离心率为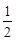 .
.
(1) 求椭圆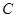 的方程; (4分)
的方程; (4分)
(2)设直线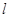 与椭圆
与椭圆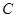 相交于
相交于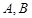 两点,以线段
两点,以线段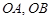 为邻边作平行四边形
为邻边作平行四边形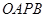 ,其中顶点
,其中顶点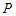 在椭圆
在椭圆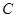 上,
上,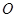 为坐标原点.求
为坐标原点.求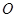 到直线
到直线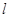 的距离的最小值. (8分)
的距离的最小值. (8分)
【答案】
(1) 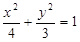 ----------------------------(4分)
----------------------------(4分)
(2)当直线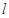 有斜率时,设
有斜率时,设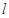 :
: ,由
,由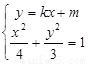 消去
消去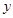 ,得
,得
 ,
,
 ㈠
㈠
设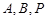 三点的坐标分别为
三点的坐标分别为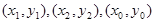 ,则以线段
,则以线段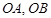 为邻边作平行四边形
为邻边作平行四边形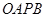 ,
,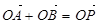 ,----------------------------------(6分)
,----------------------------------(6分)
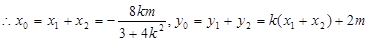
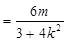
由于点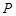 在椭圆上,所以
在椭圆上,所以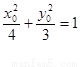 ,从而
,从而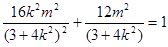 ,化简得
,化简得
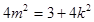 ,经检验满足㈠式
,经检验满足㈠式
又点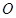 到直线
到直线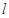 的距离为
的距离为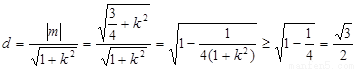
当且仅当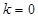 时等号成立.-------------------------------(10分)
时等号成立.-------------------------------(10分)
当直线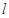 无斜率时,由对称性知,点
无斜率时,由对称性知,点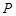 一定在
一定在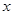 轴上,从而点
轴上,从而点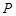 为
为 或
或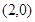 ,直线
,直线
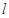 为
为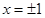 ,所以点
,所以点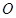 到直线
到直线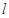 的距离为1.
的距离为1.
综上,点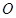 到直线
到直线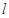 的距离的最小值为
的距离的最小值为 .--------------------------(12分)
.--------------------------(12分)
【解析】略

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目

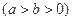 经过点
经过点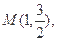 其离心率为
其离心率为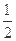
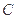 的方程
的方程 与椭圆
与椭圆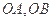 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 为坐标原点. 求
为坐标原点. 求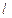 的距离的最小值.
的距离的最小值. 经过点
经过点 ,其离心率为
,其离心率为 .
. 的方程;
的方程; 与椭圆
与椭圆 两点,以线段
两点,以线段 为邻边作平行四边形
为邻边作平行四边形 ,其中顶点
,其中顶点 在椭圆
在椭圆 为坐标原点.求
为坐标原点.求