Question

在△ABC中，(1)已知b=,c=1,B=45°，求a,c,S_△ABC.

(2)已知A=60°,a=7,b=5,求c.

Answer 1

思路分析：(1)题中已知两边及一边的对角，因此用正弦定理即可；(2)题中是已知两边及其中一边所对的角，但未要求求另一边的对角，则可以用正弦定理也可用余弦定理来求解.

(1)解：由正弦定理，得.

所以sinC=.由于c＜b，则C必为锐角.

所以C=30°.

所以A=180°-B-C=180°-45°-30°=105°.

所以.

所以a=2sin105°=(或根据余弦定理求a).

所以S_△ABC=acsinB=.

(2)解法一：∵,∴.

又∵b＜a,∴B=arcsin,cosB=.

∴sinc=sin(180°-60°-B)=.

∴.

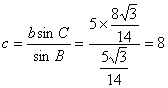解法二：因为a²=b²+c²-2bccosA，

所以49=25+c²-10ccos60°.

解得c=8或c=-3(舍去),

所以c=8.

方法归纳 由本题可以看出正弦定理与余弦定理是相通的，结合方程的思想方法，凡是能用正弦定理解的三角形，用余弦定理也能解，反之亦然.在课本中所归结的结论只是一般的求解思路.