题目内容
设p,q为实数,α,β是方程x2-px+q=0的两个实根,数列{xn}满足x1=p,x2=p2-q,xn=pxn-1-qxn-2(n=3,4,…),
(1)证明:α+β=p,αβ=q;
(2)求数列{xn}的通项公式;
(3)若p=1,q=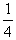 ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn.
解:(1)由求根公式,不妨设α<β,得 ,
,
∴ ,
, ;
;
(2)设 ,则
,则 ,
,
由 得
得 ,消去t,得
,消去t,得 ,
,
∴s是方程 的根,由题意可知,
的根,由题意可知, ,
,
①当α≠β时,此时方程组 的解记为
的解记为 或
或 ,
,
∴ ,
,
即 、
、 分别是公比为
分别是公比为 、
、 的等比数列,
的等比数列,
由等比数列性质可得 ,
, ,
,
两式相减,得 ,
,
 ,
,
∴ ,
,
∴ ,
,
∴ ,即
,即 ,
,
∴ ;
;
②当α=β时,即方程 有重根,∴
有重根,∴ ,
,
即 ,得
,得 ,∴s=t,
,∴s=t,
不妨设s=t=α,由①可知 ,
,
∵α=β,
∴ ,即
,即 ,
,
等式两边同时除以αn,得 ,即
,即 ,
,
∴数列 是以1为公差的等差数列,
是以1为公差的等差数列,
∴ ,
,
∴ ;
;
综上所述, ;
;
(3)把p=1, 代入
代入 ,得
,得 ,
,
解得 ,
,
∴ ,
,


 。
。
 ,
,∴
 ,
, ;
;(2)设
 ,则
,则 ,
,由
 得
得 ,消去t,得
,消去t,得 ,
,∴s是方程
 的根,由题意可知,
的根,由题意可知, ,
,①当α≠β时,此时方程组
 的解记为
的解记为 或
或 ,
,∴
 ,
,即
 、
、 分别是公比为
分别是公比为 、
、 的等比数列,
的等比数列,由等比数列性质可得
 ,
, ,
,两式相减,得
 ,
, ,
,∴
 ,
,∴
 ,
,∴
 ,即
,即 ,
,∴
 ;
;②当α=β时,即方程
 有重根,∴
有重根,∴ ,
,即
 ,得
,得 ,∴s=t,
,∴s=t,不妨设s=t=α,由①可知
 ,
,∵α=β,
∴
 ,即
,即 ,
,等式两边同时除以αn,得
 ,即
,即 ,
,∴数列
 是以1为公差的等差数列,
是以1为公差的等差数列,∴
 ,
,∴
 ;
;综上所述,
 ;
;(3)把p=1,
 代入
代入 ,得
,得 ,
,解得
 ,
,∴
 ,
,

 。
。 
练习册系列答案
相关题目
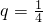 ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn.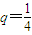 ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn.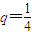 ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn.