题目内容
设p,q为实数,α,β是方程x2-px+q=0的两个实根,数列{xn}满足x1=p,x2=p2-q,xn=pxn-1-qxn-2(n=3,4,…).(1)证明:α+β=p,αβ=q;
(2)求数列{xn}的通项公式;
(3)若p=1,
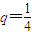 ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn.
【答案】分析:(1)设α<β,由根与系数的关系可证得答案,
(2)设xn-sxn-1=t(xn-1-sxn-2),由题意知 ,由此解得s1=α,s2=β,由此入手可以推导出{xn}的前n项和Sn.
,由此解得s1=α,s2=β,由此入手可以推导出{xn}的前n项和Sn.
(3)把p=1, 代入x2-px+q=0,得
代入x2-px+q=0,得 ,解得
,解得 ,由此可知
,由此可知 .
.
解答:解:(1)由求根公式,不妨设α<β,得
∴ ,
,
 .
.
(2)设xn-sxn-1=t(xn-1-sxn-2),则xn=(s+t)xn-1-stxn-2,由xn=pxn-1-qxn-2
得 ,
,
消去t,得s2-ps+q=0,
∴s是方程x2-px+q=0的根,由题意可知,s1=α,s2=β
①当α≠β时,此时方程组 的解为
的解为 或
或
∴xn-αxn-1=β(xn-1-αxn-2),xn-βxn-1=α(xn-1-βxn-2),
即{xn-t1xn-1}、{xn-t2xn-1}分别是公比为s1=α、s2=β的等比数列,
由等比数列性质可得xn-αxn-1=(x2-αx1)βn-2,xn-βxn-1=(x2-βx1)αn-2,
两式相减,得(β-α)xn-1=(x2-αx1)βn-2-(x2-βx1)αn-2
∵x2=p2-q,x1=p,
∴x2=α2+β2+αβ,x1=α+β
∴(x2-αx1)βn-2=β2•βn-2=βn,(x2-βx1)αn-2=α2•αn-2=αn
∴(β-α)xn-1=βn-αn,
即∴ ,∴
,∴
②当α=β时,即方程x2-px+q=0有重根,∴p2-4q=0,
即(s+t)2-4st=0,得(s-t)2=0,
∴s=t,不妨设s=t=α,由①可知xn-αxn-1=(x2-αx1)βn-2,
∵α=β,∴xn-αxn-1=(x2-αx1)αn-2=αn
即∴xn=αxn-1+αn,等式两边同时除以αn,
得 ,
,
即
∴数列 是以1为公差的等差数列,
是以1为公差的等差数列,
∴ ,
,
∴xn=nαn+αn
综上所述, .
.
 ,
,
= =
= .
.
(3)把p=1, 代入x2-px+q=0,得
代入x2-px+q=0,得 ,解得
,解得 ,∴
,∴ .
.
点评:本题考查数列性质的综合运用,解题时要认真审题,仔细计算.
(2)设xn-sxn-1=t(xn-1-sxn-2),由题意知
 ,由此解得s1=α,s2=β,由此入手可以推导出{xn}的前n项和Sn.
,由此解得s1=α,s2=β,由此入手可以推导出{xn}的前n项和Sn.(3)把p=1,
 代入x2-px+q=0,得
代入x2-px+q=0,得 ,解得
,解得 ,由此可知
,由此可知 .
.解答:解:(1)由求根公式,不妨设α<β,得

∴
 ,
, .
.(2)设xn-sxn-1=t(xn-1-sxn-2),则xn=(s+t)xn-1-stxn-2,由xn=pxn-1-qxn-2
得
 ,
,消去t,得s2-ps+q=0,
∴s是方程x2-px+q=0的根,由题意可知,s1=α,s2=β
①当α≠β时,此时方程组
 的解为
的解为 或
或
∴xn-αxn-1=β(xn-1-αxn-2),xn-βxn-1=α(xn-1-βxn-2),
即{xn-t1xn-1}、{xn-t2xn-1}分别是公比为s1=α、s2=β的等比数列,
由等比数列性质可得xn-αxn-1=(x2-αx1)βn-2,xn-βxn-1=(x2-βx1)αn-2,
两式相减,得(β-α)xn-1=(x2-αx1)βn-2-(x2-βx1)αn-2
∵x2=p2-q,x1=p,
∴x2=α2+β2+αβ,x1=α+β
∴(x2-αx1)βn-2=β2•βn-2=βn,(x2-βx1)αn-2=α2•αn-2=αn
∴(β-α)xn-1=βn-αn,
即∴
 ,∴
,∴
②当α=β时,即方程x2-px+q=0有重根,∴p2-4q=0,
即(s+t)2-4st=0,得(s-t)2=0,
∴s=t,不妨设s=t=α,由①可知xn-αxn-1=(x2-αx1)βn-2,
∵α=β,∴xn-αxn-1=(x2-αx1)αn-2=αn
即∴xn=αxn-1+αn,等式两边同时除以αn,
得
 ,
,即

∴数列
 是以1为公差的等差数列,
是以1为公差的等差数列,∴
 ,
,∴xn=nαn+αn
综上所述,
 .
. ,
,=
 =
= .
.(3)把p=1,
 代入x2-px+q=0,得
代入x2-px+q=0,得 ,解得
,解得 ,∴
,∴ .
.点评:本题考查数列性质的综合运用,解题时要认真审题,仔细计算.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
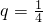 ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn.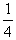 ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn. 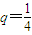 ,求{xn}的前n项和Sn.
,求{xn}的前n项和Sn.