题目内容
 如图,在正方体ABCD-A1B1C1D1中,点E、F分别在A1D、AC,且A1E=2ED,CF=2FA,则EF与BD1的位置关系是
如图,在正方体ABCD-A1B1C1D1中,点E、F分别在A1D、AC,且A1E=2ED,CF=2FA,则EF与BD1的位置关系是
- A.相交但不垂直
- B.相交且垂直
- C.异面
- D.平行
D
分析:要想判断EF与BD1的位置关系,需把它们放入同一个平面中,可连接D1E,BF,根据A1E=2ED,CF=2FA,来判断D1E,BF交与同一点,再根据成比例线段证明EF∥BD1.
解答:连接D1E,与AD交与M点处,因为A1E=2ED,可得,M为AD中点,连接BF,交AD与N点,因为CF=2FA,可得N为AD中点,所以M,N重合.且 =
= ,
,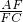 =
= .所以
.所以 =
=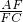 ,所以EF∥BD1
,所以EF∥BD1
故选D
点评:本题考查了立体几何中平行的判断,根据成比例线段可判断两直线平行.做题时认真分析.
分析:要想判断EF与BD1的位置关系,需把它们放入同一个平面中,可连接D1E,BF,根据A1E=2ED,CF=2FA,来判断D1E,BF交与同一点,再根据成比例线段证明EF∥BD1.
解答:连接D1E,与AD交与M点处,因为A1E=2ED,可得,M为AD中点,连接BF,交AD与N点,因为CF=2FA,可得N为AD中点,所以M,N重合.且
 =
= ,
,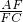 =
= .所以
.所以 =
=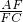 ,所以EF∥BD1
,所以EF∥BD1故选D
点评:本题考查了立体几何中平行的判断,根据成比例线段可判断两直线平行.做题时认真分析.

练习册系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )