题目内容
数列
的前n项和记为
，已知
，求
的值
由
及
，可得
．
又
时，
，则
两式相减，得
于是，数列
是以
为首项，公比为
的无穷等比数列．
进而可得，数列
是以为首项，公比为
的无穷等比数列，于是可求出极限．
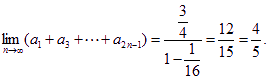
解析:
为求
当
的极限，应先求出
的表达式．从已知条件中给出与
的关系式，可以利用
，设法求出的表达式
练习册系列答案
名校课堂系列答案
相关题目
解析:
名校课堂系列答案题目内容
数列的前n项和记为，已知，求的值
由及，可得．
又时，，则
两式相减，得
于是，数列是以为首项，公比为的无穷等比数列．
进而可得，数列是以为首项，公比为的无穷等比数列，于是可求出极限．
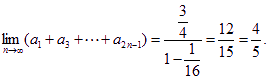
为求当的极限，应先求出的表达式．从已知条件中给出与的关系式，可以利用，设法求出的表达式
名校课堂系列答案
的前n项和记为
，
的前n项和
有最大值，且
，又
成等比数列，求
}的前n项和记为
，a1＝t，
＝2
}的前n项和
有最大值，且
＝15，又
的前n项和记为
，前
项和记为
,对给定的常数
，若
是与
无关的非零常数
，则称该数列
，求数列
是一个
“
是一个等比数列，首项
，公比
，若数列
是一个
“