题目内容
设数列{an}是等差数列,ap=q,aq=p(p≠q),求ap+q.
思路分析:a1、d是等差数列的基本元素,可先求出基本元素,得出通项公式,再求ap+q,或利用数列是特殊函数这一特点进行求解.
解法一:设{an}的公差为d,则有
∵
∴
∴an=a1+(n-1)×(-1).
∴ap+q=a1+(p+q-1)d=p+q-1+(p+q-1)×(-1)=0,
即ap+q=0.
解法二:d=![]() =
=![]() =-1,
=-1,
ap+q=ap+(p+q-p)d=q+(p+q-p)×(-1)=0.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
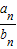 }的前n项和Sn.
}的前n项和Sn.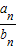 }的前n项和Sn.
}的前n项和Sn.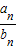 }的前n项和Sn.
}的前n项和Sn.