题目内容
设命题
：函数
在区间
上单调递减；命题
：函数
的定义域是
．如果命题
为真命题，
为假命题，求
的取值范围．
【答案】
【解析】由题意命题p或q为真命题，p且q为假命题,可知p、q一真一假.
然后分别求出p,q为真的条件，再分p真q假和p假q真两种情况分别求出a的值，再求并集即可.
解：p为真命题
在
上恒成立
在上恒成立
q为真命题
恒成立
由题意p和q有且只有一个是真命题
p真q假
p假q真
综上所述：a的范围是
练习册系列答案
相关题目
，设命题
：函数
在区间
上与
轴有两个不同的交点；命题
：
在区间
上有最小值．若
是真命题，求实数
的取值范围．
，给出下列四个命题：
上是减函数；
平移后得到函数g（x）的图象，则g（x）是偶函数；
使
，函数f（x）=
，给出下列四个命题：①函数在区间[
]上是减函数；②直线x=
是函数图象的一条对称轴；③函数f（x）的图象可由函数y=
sin2x的图象向左平移
个单位而得到；④函数y=|f（x）|的最小正周期是π；其中正确命题的序号是 ．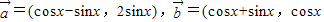
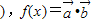，函数f（x）=
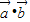，给出下列四个命题：①函数在区间[
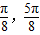]上是减函数；②直线x=
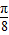是函数图象的一条对称轴；③函数f（x）的图象可由函数y=
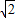sin2x的图象向左平移
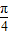个单位而得到；④函数y=|f（x）|的最小正周期是π；其中正确命题的序号是 ．