题目内容
设
 ,函数f(x)=
,函数f(x)= ,给出下列四个命题:①函数在区间[
,给出下列四个命题:①函数在区间[ ]上是减函数;②直线x=
]上是减函数;②直线x= 是函数图象的一条对称轴;③函数f(x)的图象可由函数y=
是函数图象的一条对称轴;③函数f(x)的图象可由函数y= sin2x的图象向左平移
sin2x的图象向左平移 个单位而得到;④函数y=|f(x)|的最小正周期是π;其中正确命题的序号是 .
个单位而得到;④函数y=|f(x)|的最小正周期是π;其中正确命题的序号是 .
【答案】分析:先化简f(x)= ,然后利用三角函数的性质来判断各命题的真假即可.
,然后利用三角函数的性质来判断各命题的真假即可.
解答:解:由题意知:
∵f(x)= ,所以在
,所以在 上单调递减,所以f(x)的单调递减区间为
上单调递减,所以f(x)的单调递减区间为 ,故①正确;
,故①正确;
又因为f(x)的对称轴为x= (k∈Z),即
(k∈Z),即 =
= ,则x=
,则x= ,当k=0时,x=
,当k=0时,x= ,故②正确;
,故②正确;
因为函数f(x)的图象可由函数y= sin2x的图象向左平移
sin2x的图象向左平移 个单位而得到,故③错误;
个单位而得到,故③错误;
由函数图象可知函数y=|f(x)|的最小正周期是 ,故④错误.
,故④错误.
故答案为①②.
点评:本题结合向量主要考查三角函数的性质,属基础题型.
 ,然后利用三角函数的性质来判断各命题的真假即可.
,然后利用三角函数的性质来判断各命题的真假即可.解答:解:由题意知:
∵f(x)=
 ,所以在
,所以在 上单调递减,所以f(x)的单调递减区间为
上单调递减,所以f(x)的单调递减区间为 ,故①正确;
,故①正确;又因为f(x)的对称轴为x=
 (k∈Z),即
(k∈Z),即 =
= ,则x=
,则x= ,当k=0时,x=
,当k=0时,x= ,故②正确;
,故②正确;因为函数f(x)的图象可由函数y=
 sin2x的图象向左平移
sin2x的图象向左平移 个单位而得到,故③错误;
个单位而得到,故③错误;由函数图象可知函数y=|f(x)|的最小正周期是
 ,故④错误.
,故④错误.故答案为①②.
点评:本题结合向量主要考查三角函数的性质,属基础题型.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时,t的取值范围是( )
| A、-2≤t≤2 | ||||
B、-
| ||||
| C、t≥2或t≤-2或t=0 | ||||
D、t≥
|
设奇函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,则不等式
≤0的解集为( )
| f(-x)-f(x) |
| x |
| A、(-∞,-2]∪(0,2] |
| B、[-2,0]∪[2,+∞) |
| C、(-∞,-2]∪[2,+∞) |
| D、[-2,0)∪(0,2] |
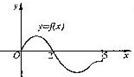 4、设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,f(x)的图象如右图,则不等式f(x)<0的解是( )
4、设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,f(x)的图象如右图,则不等式f(x)<0的解是( )