题目内容
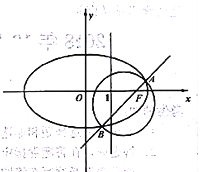
【题目】在平面直角坐标系
中，曲线
(
为参数，实数
)，曲线
(为参数，实数
)．在以
为极点，
轴的正半轴为极轴的极坐标系中，射线
与
交于，
两点，与
交于，
两点．当
时，
；当
时，
.
(Ⅰ)求
，
的值及曲线 和极坐标方程；
(Ⅱ)求
的最大值
【答案】(Ⅰ) 见解析 (Ⅱ) 
【解析】
（I）根据平方法消去参数可得到曲线C1，
的普通方程，再利用极坐标与直角坐标互化公式即可得出极坐标方程，进而得a和b的值．
（II）利用C1，C2的极坐标方程可得
，利用二倍角公式和辅助角公式进行化简，然后利用正弦函数图像的性质即可得到最大值．
(Ⅰ)由曲线
(
为参数，实数
)，
化为普通方程为
，展开为：
，
其极坐标方程为
，即
，
由题意可得当
时，
，∴
.
曲线
极坐标方程为
曲线
(为参数，实数
)，
化为普通方程为
，展开可得极坐标方程为
，
由题意可得当
时，
，∴
.
曲线极坐标方程为
(Ⅱ)由(Ⅰ)可得
，的极坐标方程分别为，.
∴
，
∵
，
∴
的最大值为，
当
，
时取到最大值.
练习册系列答案
阅读快车系列答案
相关题目
【题目】据统计，仅在北京地区每天就有500万单快递等待派送，近5万多名快递员奔跑在一线，快递网点人员流动性也较强，各快递公司需要经常招聘快递员，保证业务的正常开展．下面是50天内甲、乙两家快递公司的快递员每天送货单数统计表：
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 6 | 14 | 24 | 6 | |
已知这两家快递公司的快递员日工资方案分别为：甲公司规定底薪
元，每单抽成
元；乙公司规定底薪
元，每日前
单无抽成，超过单的部分每单抽成
元．
（1）分别求甲、乙快递公司的快递员的日工资
（单位：元）与送货单数
的函数关系式；
（2）小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作，如果仅从日收入的角度考虑，以这50天的送货单数为样本，将频率视为概率，请你利用所学的统计学知识为他作出选择，并说明理由．
