题目内容
如图，在△ABC中，DE∥BC，DF∥AC，AE：AC=3：5，DE=6，则BF=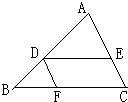
分析：因为已知中有两个平行关系，我们可以大胆猜想，本题的解答过程一定与平行线分线段成比例定理有关，因此可以根据平行线分线段成比例定理，构建比例式，列出已知线段与未知线段之间的关系式，解方程进行求解．
解答：解：因为DE∥BC，则△ADE～△ABC，
所以
=
，即
=
，所以BC=10．
又DF∥AC，则四边形DECF是平行四边形，
故BF=BC-FC=BC-DE=10-6=4．
所以
| AE |
| AC |
| DE |
| BC |
| 3 |
| 5 |
| 6 |
| BC |
又DF∥AC，则四边形DECF是平行四边形，
故BF=BC-FC=BC-DE=10-6=4．
点评：当题目中出现有多个平行关系时，我们可以使用平行线分线段成比例定理构造比例式，表示已知线段与未知线段之间的关系，解方程即可求解．解题思路是：分析已知量与未知量之间的关系，选择适合的性质构建方程，解方程求解．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知