题目内容
已知椭圆C: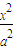 +
+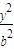 =1(a>b>0)的上顶点为P(0,1),过C的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆C上,该菱形对角线BD所在直线的斜率为-1.
=1(a>b>0)的上顶点为P(0,1),过C的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆C上,该菱形对角线BD所在直线的斜率为-1.(1)求椭圆∑的方程;
(2)当直线BD过点(1,0)时,求直线AC的方程;
(3)当∠ABC=
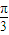 时,求菱形ABCD面积的最大值.
时,求菱形ABCD面积的最大值.
【答案】分析:(1)依题意,b=1,解 ,得|y|=
,得|y|= ,所以
,所以 ,由此能求出椭圆E的方程.
,由此能求出椭圆E的方程.
(2)直线BD:y=-1×(x-1)=-x+1,设AC:y=x+b,由方程组 得
得 ,再由根的判别式、中点坐标公式和菱形的性质能推导出AC的方程.
,再由根的判别式、中点坐标公式和菱形的性质能推导出AC的方程.
(3)因为四边形ABCD为菱形,且 ,所以AB=AC=BC,所以菱形ABCD的面积
,所以AB=AC=BC,所以菱形ABCD的面积 ,由AC2=(x2-x1)2+(y2-y1)2=2(x2-x1)2=2(x2+x1)2-8x1x2=
,由AC2=(x2-x1)2+(y2-y1)2=2(x2-x1)2=2(x2+x1)2-8x1x2= ,能推导出当且仅当b=0时,菱形ABCD的面积取得最大值.
,能推导出当且仅当b=0时,菱形ABCD的面积取得最大值.
解答:解:(1)依题意,b=1,
解 ,得|y|=
,得|y|= ,
,
所以 ,a=2,
,a=2,
椭圆E的方程为 .
.
(2)直线BD:y=-1×(x-1)=-x+1,
设AC:y=x+b,
由方程组 得
得 ,
,
当 时,
时,
A(x1,y1),C(x2,y2)的中点坐标为 =-
=- ,
, ,
,
ABCD是菱形,所以AC的中点在BD上,所以
解得 ,满足△=5-b2>0,所以AC的方程为y=x-
,满足△=5-b2>0,所以AC的方程为y=x- .
.
(3)因为四边形ABCD为菱形,且 ,所以AB=AC=BC,所以菱形ABCD的面积
,所以AB=AC=BC,所以菱形ABCD的面积 ,
,
由(2)可得AC2=(x2-x1)2+(y2-y2)2=2,
AC2=(x2-x1)2+(y2-y1)2=2(x2-x1)2=2(x2+x1)2-8x1x2=2× =
= ,
,
因为 ,所以当且仅当b=0时,菱形ABCD的面积取得最大值,最大值为
,所以当且仅当b=0时,菱形ABCD的面积取得最大值,最大值为 .
.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要灵活运用根的判别式、中点坐标公式和菱形的性质,结合椭圆的性质注意合理地进行等价转化.
 ,得|y|=
,得|y|= ,所以
,所以 ,由此能求出椭圆E的方程.
,由此能求出椭圆E的方程.(2)直线BD:y=-1×(x-1)=-x+1,设AC:y=x+b,由方程组
 得
得 ,再由根的判别式、中点坐标公式和菱形的性质能推导出AC的方程.
,再由根的判别式、中点坐标公式和菱形的性质能推导出AC的方程.(3)因为四边形ABCD为菱形,且
 ,所以AB=AC=BC,所以菱形ABCD的面积
,所以AB=AC=BC,所以菱形ABCD的面积 ,由AC2=(x2-x1)2+(y2-y1)2=2(x2-x1)2=2(x2+x1)2-8x1x2=
,由AC2=(x2-x1)2+(y2-y1)2=2(x2-x1)2=2(x2+x1)2-8x1x2= ,能推导出当且仅当b=0时,菱形ABCD的面积取得最大值.
,能推导出当且仅当b=0时,菱形ABCD的面积取得最大值.解答:解:(1)依题意,b=1,
解
 ,得|y|=
,得|y|= ,
,所以
 ,a=2,
,a=2,椭圆E的方程为
 .
.(2)直线BD:y=-1×(x-1)=-x+1,
设AC:y=x+b,
由方程组
 得
得 ,
,当
 时,
时,A(x1,y1),C(x2,y2)的中点坐标为
 =-
=- ,
, ,
,ABCD是菱形,所以AC的中点在BD上,所以

解得
 ,满足△=5-b2>0,所以AC的方程为y=x-
,满足△=5-b2>0,所以AC的方程为y=x- .
.(3)因为四边形ABCD为菱形,且
 ,所以AB=AC=BC,所以菱形ABCD的面积
,所以AB=AC=BC,所以菱形ABCD的面积 ,
,由(2)可得AC2=(x2-x1)2+(y2-y2)2=2,
AC2=(x2-x1)2+(y2-y1)2=2(x2-x1)2=2(x2+x1)2-8x1x2=2×
 =
= ,
,因为
 ,所以当且仅当b=0时,菱形ABCD的面积取得最大值,最大值为
,所以当且仅当b=0时,菱形ABCD的面积取得最大值,最大值为 .
.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要灵活运用根的判别式、中点坐标公式和菱形的性质,结合椭圆的性质注意合理地进行等价转化.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为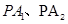 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.