��Ŀ����
��b��0,��Բ����Ϊ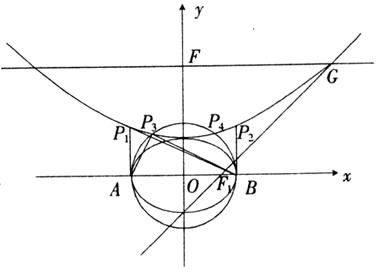
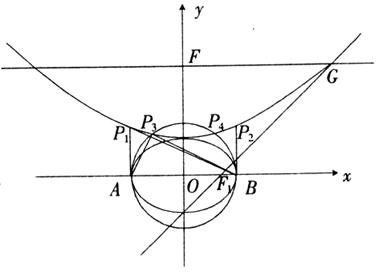
ͼ4
(1)��������������Բ���̺������߷���.
(2)��A��B�ֱ�����Բ��������Ҷ˵�,��̽�������������Ƿ���ڵ�P,ʹ�á�ABPΪֱ��������?������,��ָ�����м��������ĵ�?��˵������(���ؾ��������Щ�������).
��:(1)�� ,
,
�õ�G������Ϊ(4,b+2),
�������ڵ�G��������б��Ϊk=![]()
�������ڵ�G�������߷���Ϊx-4=![]() ��y=x+b-2,
��y=x+b-2,
��F1������Ϊ(b,0),4b=8(![]() -b),
-b),
��b=1.
��Բ����Ϊ![]() +y2=1,�����ߵķ���Ϊx2=8(y-1).
+y2=1,�����ߵķ���Ϊx2=8(y-1).
(2)�����ĸ���.

�ֱ��A��B��x��Ĵ��߽���������P1��P2,
��õ�����ֱ�������Ρ�ABP1����ABP2.
��ABΪֱ����Բ��Ȼ������������������P3��P4,
���ֵõ�����ֱ�������Ρ�ABP3����ABP4.
��ΪP
����P3��P1���غϣ�ͬ��P4��P2���غ�.
��P1��P2��P3��P4������������ͬ�ĵ㡣

��ϰ��ϵ�д�
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
�����Ŀ