题目内容
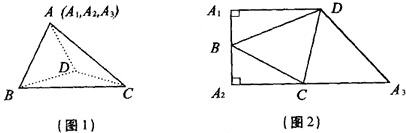
已知四面体ABCD(图1),将其沿AB,AC,AD剪开,展成的平面图形正好是图2所示的直角梯形A1A2A3D(梯形的顶点A1,A2,A3重合于四面体的顶点A).
(1)证明:AB⊥CD.
(2)当A1D=10,A1A2=8时,求四面体ABCD的体积.

(1)在四面体ABCD中,
 ⇒AB⊥平面A
⇒AB⊥平面A![]() CD⇒AB⊥CD.
CD⇒AB⊥CD.
(2)在题图2中作DE⊥A2A3于E.

因为A1A2=8,所以DE=8.
又因为A1D=A3D=10,
所以EA3=6,A2A3=10+6=16.
又A2C=A3C,所以A3C=8,
即题图1中AC=8,AD=10,
由A1A2=8,A1B=A2B得题图1中AB=4,![]()
所以S△ACD=![]() =
=![]() DE·A3C=
DE·A3C=![]() ×8×8=32.
×8×8=32.
又因为AB⊥平面ACD,
所以VB-ACD=![]() ×32×4=
×32×4=![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知四面体ABCD中,AB=AD=6,AC=4,CD=2
,AB⊥平面ACD,则四面体ABCD外接球的表面积为( )
| 13 |
| A、36π | B、88π |
| C、92π | D、128π |
 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3 已知四面体ABCD中,
已知四面体ABCD中,