题目内容
设椭圆
过点
，且焦点为
。
（1）求椭圆
的方程；
（2）当过点
的动直线
与椭圆相交与两不同点A、B时，在线段
上取点
，
满足
，证明：点总在某定直线上。
过点，且焦点为。（1）求椭圆
的方程；（2）当过点
的动直线与椭圆相交与两不同点A、B时，在线段上取点，满足
，证明：点总在某定直线上。（1）所求椭圆方程为 
（2）证明见解析
（2）证明见解析
（1）由题意：
，解得
，
所求椭圆方程为
（2）解：设过P的直线方程为：
，
设
，
，
则
，
∵
，∴
，即
，
化简得：
，
∴
，
去分母展开得：
化简得：
，解得：
又∵Q在直线上，
∴
，∴
即
，
∴Q恒在直线
上。
，解得，所求椭圆方程为
（2）解：设过P的直线方程为：
，设
，，则
，∵
，∴，即，化简得：
，∴
，去分母展开得：
化简得：
，解得：又∵Q在直线
上，∴
，∴即
，∴Q恒在直线
上。
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
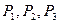，使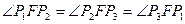
，
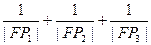为定值，并求此定值。(8分)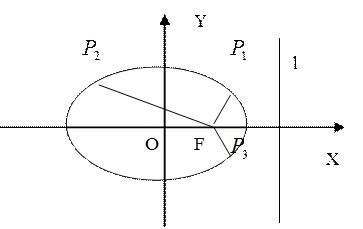
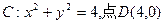，坐标原点为O.圆C上任意一点A在x轴上的射影为点B，已知向量
.
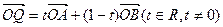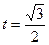时，设动点Q关于x轴的对称点为点P，直线PD交轨迹E于点F（异于P点），证明：直线QF与x轴交于定点，并求定点坐标.
+
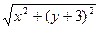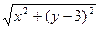=10为不含根式的形式是( )
+
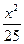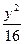="1"
=1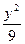
+
="1"
+
+
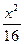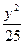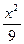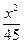=1的两个焦点分别为F1、F2，P为椭圆上一点，且PF1⊥PF2，则||PF1|-|PF2||的值为（ ）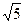
+
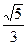
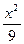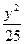=1上到两个焦点距离之积最大的点的坐标是_______________.
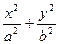=1(a>b>0)的内接矩形面积的最大值.
;
;
.
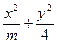=1的焦距为2,则m的值等于__________________.