题目内容
某旅游公司为三个旅游团提供了甲,乙,丙,丁4条旅游线路,每个旅游团从中任选一条线路.
(1)求恰有2条线路没有被选的概率;
(2)设选择甲线路的旅游团的个数为ξ,求Eξ及Dξ.
(1)求恰有2条线路没有被选的概率;
(2)设选择甲线路的旅游团的个数为ξ,求Eξ及Dξ.
分析:(1)3个旅游团选择旅游线路的所有方法有43种,满足条件的选法有C42•C32•A22 种.代入概率公式得P(A)=
=
(2)先判定随机变量的取值,然后结合题意求出每种情况的概率,求出随机变量的分布列,利用分布列求出数学期望和方差.
| ||||||
| 43 |
| 9 |
| 16 |
(2)先判定随机变量的取值,然后结合题意求出每种情况的概率,求出随机变量的分布列,利用分布列求出数学期望和方差.
解答:解:(1)记“恰有2条线路没有被选”为事件A,3个旅游团选择旅游线路的所有方法有43种,
恰有2条线路没有被选的有C42•C32•A22 种,则恰有2条线路没有被选的概率P(A)=
=
(6分)
(2)ξ的可能取值为0,1,2,3(7分)
则P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
,(9分)
故ξ的分布列为
Eξ=0×
+1×
+2×
+3×
=
(11分)
Dξ=(0-
)2×
+(1-
)2×
+(2-
)2×
+(3-
)2×
=
(13分)
恰有2条线路没有被选的有C42•C32•A22 种,则恰有2条线路没有被选的概率P(A)=
| ||||||
| 43 |
| 9 |
| 16 |
(2)ξ的可能取值为0,1,2,3(7分)
则P(ξ=0)=
| 33 |
| 43 |
| 27 |
| 64 |
| ||
| 43 |
| 27 |
| 64 |
| ||
| 43 |
| 9 |
| 64 |
| 1 |
| 43 |
| 1 |
| 64 |
故ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 64 |
| 1 |
| 64 |
| 3 |
| 4 |
Dξ=(0-
| 3 |
| 4 |
| 27 |
| 64 |
| 3 |
| 4 |
| 27 |
| 64 |
| 3 |
| 4 |
| 9 |
| 64 |
| 3 |
| 4 |
| 1 |
| 64 |
| 9 |
| 16 |
点评:本题主要考查概率与统计的内容,利用概率公式分别求出概率,然后求出概率的分布列,利用分布列求期望,考查学生的运算能力,综合性较强.

练习册系列答案
相关题目
 四条旅游线路,每个旅游团可任选其中一条线路,则选择
四条旅游线路,每个旅游团可任选其中一条线路,则选择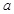 线路旅游团数
线路旅游团数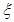 的数学期望
的数学期望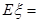 ;
;